7.3 Приклад виконання завдання

 

Кривошипно-шатунний механізм (рис. 7.4) складається з кривошипа ОА=40 см, шатуна АВ і повзуна В. Точка С належить ланці АВ і АС=20 см.

У даний момент часу, в даному положенні механізму кутова швидкість кривошипа ω_ОА=5 рад/с, кутове прискорення ε_ОА=10 рад/с².

Визначити для заданого положення механізму швидкості й прискорення точок А, В, С ланки АВ, а також її кутову швидкість ω_АВ і кутове прискорення ε_АВ.

 

Розв’язання

1. Ланка ОА виконує обертальний рух навколо нерухомої точки О. Тоді

.

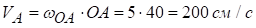Вектор 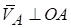 і спрямований у бік обертання ОА, у бік обертання ω.

Повзун В виконує поступальний рух, тому напрямок швидкості точки В, яка також належить ланці АВ, відомий і спрямований уздовж траєкторії руху точки В.

Шатун АВ рухається  плоскопаралельно з миттєвим центром швидкості в точці Р. Точка Р є точкою перетину перпендикулярів до напрямку швидкостей у точках А і В.

 

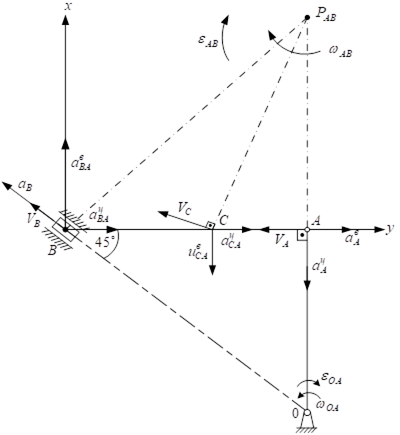
Рисунок 7.4

 

Кутова швидкість ланки АВ

,

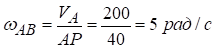де АР=АВ=ОА, тому що /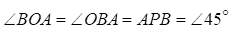

Кутова швидкість ланки АВ спрямована відповідно до того, як вектор  обертається навколо МЦШ.

Швидкості точок В і С ланки АВ:

,

.

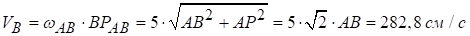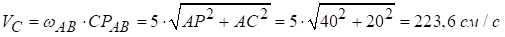Відповідно 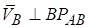,  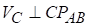і спрямовані у бік обертання .

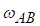2. Визнаємо прискорення точок А, В, С ланки АВ.

Прискорення точки А по належності її  ланці ОА, що виконує обертальний рух навколо нерухомої осі, складається з геометричної суми обертального і доцентрового прискорень:

,

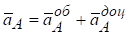де 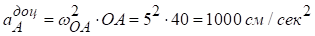 ‑ доцентрове прискорення точки А, спрямоване уздовж АО від А до О,

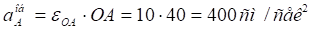 ‑ обертальне прискорення точки А, спрямоване відповідно до напрямку кутового прискорення  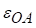і вектор .

; .

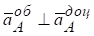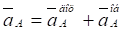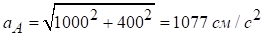Припустимо, що повзун В рухається прискорено. Тоді напрямок прискорення 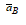 співпадає з напрямком швидкості 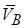. Визначаємо полюсом точку А.

Прискорення точки В визначається за формулою

 

,

 

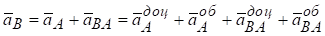де 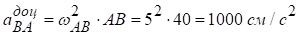 ‑ доцентрове прискорення точки В відносно точки А, спрямоване від точки В до точки А, уздовж АВ

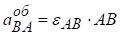 ‑ обертальне прискорення точки В відносно точки А, спрямоване перпендикулярно до АВ і 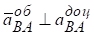, відоме за напрямком. При цьому припускаємо, що кутове прискорення ланки АВ  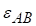співпадає за напрямком обертання з кутовою швидкістю .

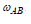Обираємо систему координат xВy (рис. 7.4) і проектуємо геометричне рівняння прискорення точки В, 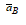 на осі координат:

 

У: ,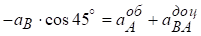

Х:.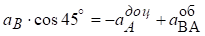

 

У цій системі двох алгебраїчних рівнянь є два невідомі прискорення 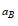точки В  і прискорення .

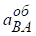Обчислюємо їх:

,

.

 

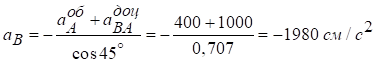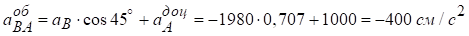Знак мінус у знайдених відповідях означає, що насправді вектори прискорень 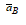 і 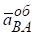 спрямовані у бік, протилежний зазначеному на рисунку, тобто прискорення точки В протилежне напрямку швидкості .

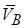Кутове прискорення ланки АВ:

 

.

 

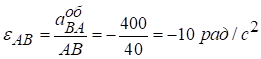Знак мінус означає, що кутове прискорення ланки АВ протилежне кутовій швидкості 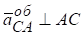 за напрямком обертання.

Прискорення точки С ланки АВ визначаємо за цією ж методикою:

 

.

 

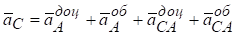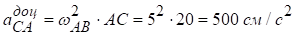 і напрямлено вздовж АС від С до А.

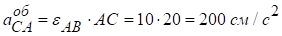 і спрямоване у бік дійсного спрямування  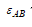таким чином, щоб .

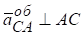Геометричне рівняння з визначення 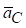 проектуємо на осі у і х:

 

У: ,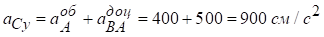

Х: ,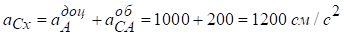

 

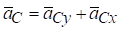 ‑ діагональ прямокутника, побудованого на складових .

 

.

 

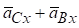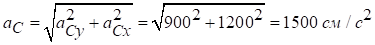Відповідь:V_A=200 cм/с, a_A=1077 см/с², ω_AB=5 рад/с, V_B=282,8 cм/с, a_B=1980 см/с², V_c=223,6 cм/с, a_c=1500 см/с², ε_AB=10 рад/с².