8 ДИНАМІКА ТОЧКИ

 

 

8.1 Теоретичні відомості і методичні вказівки

 

Сила – це міра механічного прояву фізичного впливу на матеріальні тіла. Сила, як векторна величина, підпорядкована всім законам векторного числення.

Основні види сил: сила тяжіння ( 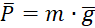, або 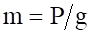); сила тертя ( 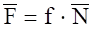); сила пружності (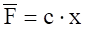, де с ‑ коефіцієнт жорсткості [H / м]); сила в’язкого тертя (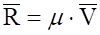), сили аеродинамічного (гідродинамічного) опору.

Одиницею виміру сили є Н (Ньютон) – це сила, яка надає масі в 1 кілограм прискорення в . .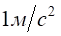

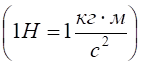Незалежним первинним поняттям в теоретичній механіці є маса. Під масою розуміють інертність тіла. З іншого боку, масу можна визначити як кількість речовин в тілі, що пропорційна його вазі (“гравітаційна маса”). У теоретичній механіці приймається, що маса не змінюється за часом, її величина не залежить ні від швидкості точки, ні від її положення у просторі.

Матеріальна точка – це матеріальне тіло (тіло, що має масу), розмірами якого при вивченні його руху можна знехтувати.

Закони динаміки.

Перший закон Ньютона (закон інерції).

Ізольована матеріальна точка зберігає стан спокою або рівномірного і прямолінійного руху доти, доки вплив з боку інших сил не виведе її з цього стану.

Другий закон Ньютона (основний закон динаміки).

Швидкість зміни кількості руху матеріальної точки дорівнює силі, що діє на цю точку. Прискорення матеріальної точки пропорційне прикладеній до неї сили і має однаковий з нею напрям:

 

 

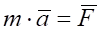
Третій закон Ньютона (закон рівності дії та протидії)

Сили взаємодії двох матеріальних точок або двох тіл (дія і протидія) рівні за величиною, напрямлені в протилежні боки і мають загальну лінію дії.

Четвертий закон Ньютона (принцип суперпозиції)

Прискорення матеріальної точки, що виникає при одночасній дії декількох сил, дорівнює векторній сумі прискорень, які надають точці окремі сили.

Дві основні задачі динаміки:

Перша або пряма основна задача динаміки: знаючи закон руху точки і її масу, визначити сили, що викликають цей рух.

Якщо рух матеріальної точки масою m задано координатним способом x=f₁(t), y=f₂(t), z=f₃(t), то:

1. Диференціюючи двічі ці співвідношення за часом, одержимо проекції  прискорень на координатні осі:

 

                                       

 

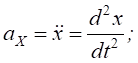
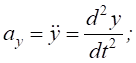
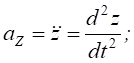
2. Використовуючи динамічні рівняння руху матеріальної точки в координатній формі , визначимо проекції сили:

 

                                               

 

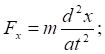
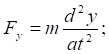
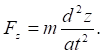
3. Знаходимо модуль рівнодійної сили .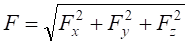

4. Напрям  рівнодійної сили визначимо за направленими косинусами

 

                           .

 

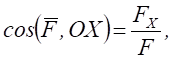
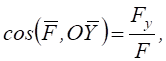
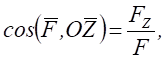Друга  або обернена задача динаміки: визначити кінематичні рівняння руху точки, якщо відомі її маса m, прикладені до неї сили 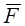 і початкові умови руху.

Розв’язання другої задачі динаміки зводиться до інтегрування диференційних рівнянь руху матеріальної точки.

1. Складання динамічних рівнянь руху матеріальної точки згідно з умовами задачі (спочатку знаходять проекції сил F на осі координат (F_x, F_y F_z)).

2. Інтегрування одержаної системи диференційних рівнянь.

3. Визначення значень сталих інтегрування. Сталі інтегрування визначають з початкових умов. Початкові умови – це величини, що визначають положення точки і проекції вектора швидкості в початковий момент часу (t=t)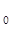

4. Знаходження закону руху : x = x(t);  y = y(t);  z = z(t).

 

Питання для самоперевірки знань

та контролю засвоєння матеріалу

 

1. Які закони лежать в основі динаміки?

2. Що називають матеріальною точкою?

3. Що таке сила?

4. Основні види сил.

5. Дати означення маси, що прийнята в механіці.

6. Як отримують диференціальні рівняння руху вільної та невільної матеріальної точки?

7. У чому суть першої та другої задач динаміки?