
|
ТЕОРЕТИЧНА ТА ПРИКЛАДНА МЕХАНІКА
|

|
ТЕОРЕТИЧНА ТА ПРИКЛАДНА МЕХАНІКА
|
8.3 Приклад виконання завдання
Приклад 1. Вантаж масою m підіймається по шорсткій похилій площині (рис. 8.2), що складає кут α=300 з горизонтом. В початковий момент швидкість вантажу дорівнювала υ0=15 м/с. Коефіцієнт тертя f=0,1. Який шлях пройде вантаж до зупинки? За який час вантаж пройде цей шлях?
Розв’язання
Для дослідження руху вантажу запишемо диференціальне рівняння невільного вантажу в проекціях на вісь х.
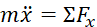 (8.1)
(8.1)
Вантаж переміщується під дією ваги P, нормальної складової N та сили тертя Fтр шорсткої поверхні.
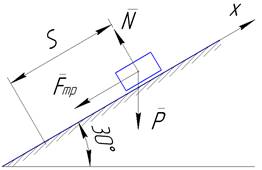
Рисунок 8.2
Враховуючи сили, що прикладені до вантажу (рис. 8.2), рівняння (8.1) запишеться в вигляді:
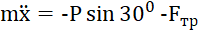 (8.2)
(8.2)
Вага вантажу біля поверхні Землі.
P = mg (8.3)
На підставі закону Амонтона-Кулона при критичній рівновазі вантажу отримаємо:
Fтр= f N (8.4)
Так як вантаж рухається вздовж осі х, тоді:
N = P cos 300 (8.5)
Підставимо формули (8.3), (8.4) та (8.5) в диференціальне рівняння (8.2)
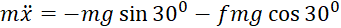 ;
; 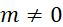 (8.6)
(8.6)
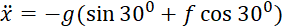 (8.7)
(8.7)
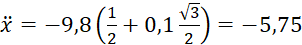 (8.8)
(8.8)
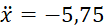 (8.9)
(8.9)
2) Інтегруємо диференційне рівняння (8.9) двічі:
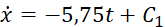 (8.10)
(8.10)
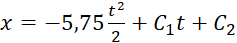 (8.11)
(8.11)
3) Для визначення постійних інтегрування в рівняннях (8.10) та (8.11) скористаємось початковими умовами: при t=0; 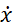 0=15м/c; х0=0.
0=15м/c; х0=0.
Отже С1=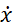 0; С2=х0 ; С1=15 ; С2=0, тоді
0; С2=х0 ; С1=15 ; С2=0, тоді
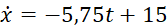 . (8.12)
. (8.12)
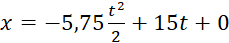 . (8.13)
. (8.13)
4) Для моменту τ, коли вантаж зупиниться, 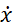 =0 х=S, тоді
=0 х=S, тоді
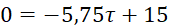 . (8.14)
. (8.14)
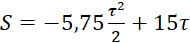 . (8.15)
. (8.15)
З формули (8.14) знаходимо τ:
τ = 15 / 5,75 = 2,61с . (8.16)
Підставимо значення τ (8.16) в рівняння (8.15) і отримаємо шлях, який пройде вантаж до зупинки
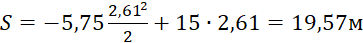 .
.
Відповідь: τ = 2,61с; S = 19,57м.
Приклад 2. Матеріальна точка m рухається під дією сили 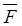 на ділянці АВ (рис. 8.3). Знайти час τ руху точки та відстань DC, якщо: m=5 кг, VA=3 м/с, F=30H, d= 4 м, АВ=11м.
на ділянці АВ (рис. 8.3). Знайти час τ руху точки та відстань DC, якщо: m=5 кг, VA=3 м/с, F=30H, d= 4 м, АВ=11м.
Розв’язання
Точка на ділянці АВ рухається під дією сили ваги P,постійної сили F реакції N гладенької поверхні. Запишемо диференціальне рівняння руху точки в проекціях на вісь η.
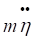 =F+Psin150,
=F+Psin150,
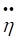 =
=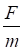 +g∙sin150.
+g∙sin150.
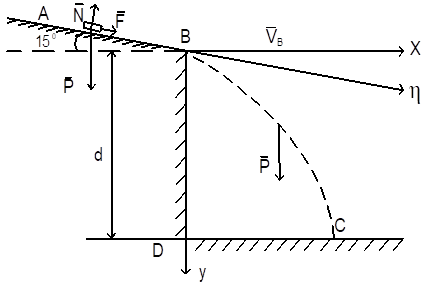
Рисунок 8.3
Початкові умови руху точки: при t=0; η=VA; η=0.
Граничні умови: при t=τ с; η=VB; η=AB.
Інтегруємо диференціальне рівняння руху точки, враховуючі початкові та граничні умови руху точки.
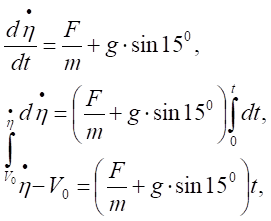
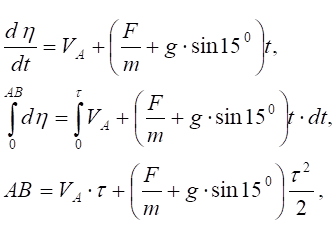
або
4,27∙τ2+3τ-11= 0,
Звідки:
τ1,2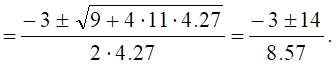
Так як τ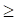 0, то час руху точки на ділянці АВ: τ = 1,28 с.
0, то час руху точки на ділянці АВ: τ = 1,28 с.
Визначимо швидкість точки в пункті В.
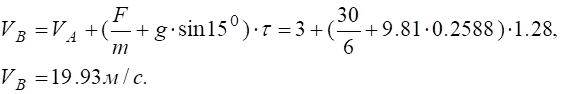
Розглянемо рух точки на ділянці ВС (рис. 8.3).
Запишемо диференціальні рівняння руху точки в проекціях на осі x та y
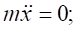
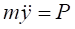 .
.
Так як точка має масу, то:
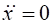 ,
, 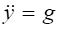 . (8.17)
. (8.17)
Початкові умови руху точки: при t=0;
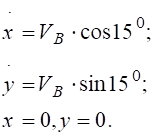 8.18)
8.18)
Граничні умови: при t = t1; y = d; x = DC.
Інтегруємо друге диференціальне рівняння системи (8.17).
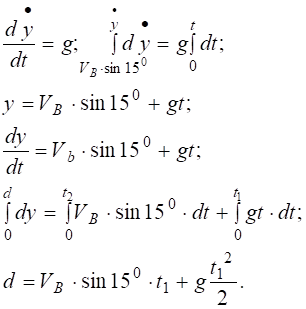
Підставляючи дані, отримаємо:
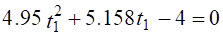 .
.
Тоді 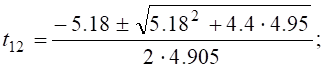 Звідки t1 =0,52 c.
Звідки t1 =0,52 c.
З першого диференціального рівняння системи (8.17) 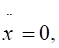 та початкових умов маємо:
та початкових умов маємо: 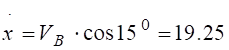 м/с.
м/с.
Другий раз інтегруємо рівняння 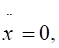 враховуючи початкові (8.18) та граничні умови руху точки на ділянці ВС (рис. 8.3).
враховуючи початкові (8.18) та граничні умови руху точки на ділянці ВС (рис. 8.3).
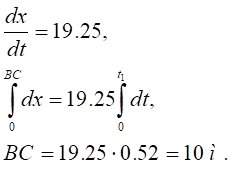
Відповідь: τ = 0,52 c., ВС = 10 м.