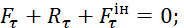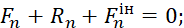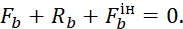9 МЕТОД КІНЕТОСТАТИКИ

9.1 Теоретичні відомості і методичні вказівки

9.1.1 Принцип Д’Аламбера

Розглянуті вище рівняння руху матеріальних об’єктів (матеріальних точок)  виходять безпосередньо з законів Галілея-Ньютона.

Але є багато таких інженерних задач динаміки, розв’язання яких методами ньютонівської механіки потребує дуже великих зусиль, а інколи і взагалі неможливе. В таких випадках користуються методами іншої, так званої аналітичної механіки, в основу яких покладено принципи, відмінні від ньютонівських. Засновником цієї ланки механіки був Лейбниць.

Для спрощення, щоб не виходити за межі ньютоновської механіки, будемо розглядати ці принципи як такі, що є наслідками законів класичної механіки з додаванням до них аксіоми про звільнення від в’язей. В той же час потрібно розуміти, що це не теореми, які доводяться за допомогою законів Галілея-Ньютона, а саме принципи. Якщо взяти їх за основу, можна отримати і закони Ньютона, і всю ньютонівську механіку.

Розробниками основних принципів аналітичної механіки були французькі вчені Д’Аламбер (1717-1783) і Лагранж (1736-1813).

Принцип  Д’Аламбера дозволяє приводити всі задачі, які відносяться до руху тіл, до більш простої задачі про рівновагу.

Сучасне трактування принципу Д’Аламбера з використанням поняття сили інерції, яке було введено в механіку на початку ХІХ століття, є фундаментом важливого метода технічної механіки – метода кінетостатики.

9.1.2 Принцип Д’Аламбера для матеріальної точки

Принцип Д’Аламбера дає можливість врівноважити систему сил: для невільної матеріальної точки в кожний момент часу сума активних сил, що прикладені до точки, реакції в¢язів і сил інерції дорівнює нулю:

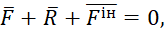
де 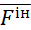 ,  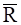– рівнодійні активних сил і сил інерції, прикладених до точки;

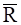 – реакція в¢язей.

Тобто рівняння руху записується у вигляді умови рівноваги статики.

Силою інерції 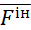 – матеріальної точки називається вектор, який дорівнює за модулем добутку маси точки на її прискорення і спрямований у бік, протилежний прискоренню точки: 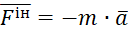. Її називають даламберовою силою інерції.

При координатному способі задання руху в системі відліку 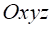 векторне рівняння  переходить в систему скалярних рівнянь:

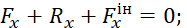
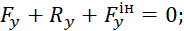
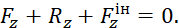
Якщо ж рух точки задано натуральним способом, то будемо мати систему таких рівнянь: