2.7 Експертні оцінки, рангова кореляція і конкордація
Нехай у процесі системного аналізу нам довелося враховувати деяку величину U, вимірювання якої можливе лише за порядковою шкалою (Ord). Наприклад, нам доводиться враховувати 10 цілей функціонування системи і потрібно з’ясувати їх відносну значимість, тобто, питому вагу.
Якщо існує група осіб, компетентність яких у даній області не викликає сумнівів, то можна опитати кожного з експертів, запропонувавши їм розташувати цілі по важливості або «проранжувати» їх. У найпростішому випадку можна не дозволяти повторювати ранги, хоча це не обов’язково – повторення рангів завжди можна врахувати. Результати експертної оцінки в нашому прикладі опишемо табл.. 2.3 рангів цілей:
| Експерти | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сума |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 3 | 5 | 1 | 8 | 7 | 10 | 9 | 2 | 4 | 6 | 55 |
| B | 5 | 1 | 2 | 6 | 8 | 9 | 10 | 3 | 4 | 7 | 55 |
| Сума рангів | 8 | 6 | 3 | 14 | 15 | 19 | 19 | 5 | 8 | 13 | |
| Сумарний ранг | 4.5 | 3 | 1 | 7 | 8 | 9.5 | 2 | 4.5 | 6 | 55 |
Отже, для кожної з цілей Ti ми можемо знайти суму рангів, що визначені експертами, а потім сумарний або результуючий ранг мети Ri. Якщо суми рангів збігаються – призначається середнє значення.
Метод рангової кореляції дозволяє відповісти на запитання – наскільки корельовані, невипадкові ранжировки кожного з двох експертів, а значить – наскільки можна довіряти результуючим рангам?
Зазвичай, висувається основна гіпотеза – про відсутність зв’язку між ранжировками і встановлюється ймовірність справедливості цієї гіпотези. Для цього можна використовувати два підходи: визначення коефіцієнтів рангової кореляції Спірмена або Кенделла.
Простішим у реалізації є перший метод, за яким обчислюється значення коефіцієнта Спірмена.
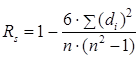, (2.40)
де di визначаються різницями рангів першої і другої ранжировок по n об’єктів у кожній.
У нашому прикладі сума квадратів різниць рангів складає 30, а коефіцієнт кореляції Спірмена близько 0.8, що дає значення ймовірності гіпотези про повну незалежність двох ранжировок усього лише 0.004.
При необхідности можна скористатися послугами групи з m експертів, встановити результуючі ранги цілей, але тоді виникне питання про узгодженість думок цих експертів або конкордації.
Нехай у нас є ранжировки 4 експертів стосовно 6 факторів, що визначають ефективність деякої системи (див. у таблиці нижче).
Відзначимо, що повна сума рангів складає 84, що дає у середньому по 14 на фактор. Для загального випадку n факторів і m експертів середнє значення суми рангів для будь-якого фактора визначиться виразом:
Δ = 0.5 ∙ m ∙ (n + 1), (2.41)
Тепер можна оцінити ступінь узгодженості думок експертів щодо шести факторів. Для кожного з факторів спостерігається відхилення суми рангів, зазначених експертами, від середнього значення такої суми (табл. 2.4).
| Фактори Експерти |
1 | 2 | 3 | 4 | 5 | 6 | Сума |
|---|---|---|---|---|---|---|---|
| A | 5 | 4 | 1 | 6 | 3 | 2 | 21 |
| B | 2 | 3 | 1 | 5 | 6 | 4 | 21 |
| C | 4 | 1 | 6 | 3 | 2 | 5 | 21 |
| D | 4 | 3 | 2 | 3 | 2 | 5 | 21 |
| Сума рангів Сум. ранг |
15 4 |
11 2 |
10 1 |
19 6 |
12 3 |
17 5 |
84 |
| Відхилення суми Від середнього |
+1 1 |
-3 9 |
-4 16 |
+5 25 |
-2 4 |
+3 9 |
0 64 |
Оскільки сума цих відхилень завжди дорівнює нулю, для їх усереднення розумним буде використовувати квадрати значень.
У нашому випадку сума таких квадратів складе S=64, а в загальному випадку ця сума буде найбільшою тільки при повному збігу думок всіх експертів стосовно всіх факторів:
Smax = m2 (n3 – n) / 12, (2.42)
М. Кенделлом запропоновано показник узгодженості або коефіцієнт конкордації, що визначається як:
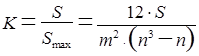, (2.43)
У нашому прикладі значення коефіцієнта конкордації складає близько 0.229, що для чотирьох експертів і шести факторах достатньо, щоб з ймовірістю не більше 0.05 вважати думки експертів неузгодженими. Справа у тому, що саме випадковість ранжировок, їх некорельованість прораховується досить просто. Так, для нашого прикладу, зазначена ймовірність відповідає сумі квадратів відхилень S = 142.3, що набагато більше 64.
На закінчення питання про особливості методу експертних оцінок у системному аналізі відзначимо ще дві таких обставини.
У першому прикладі ми одержали результуючі ранги 10 цілей функціонування системи. Як скористатися цим і як перейти від рангової (Ord) шкали цілей до шкали вагових коефіцієнтів, тобто, у діапазоні від 0 до 1? Тут звичайно використовуються елементарні прийоми нормування. Якщо ціль 3 має ранг 1, ціль 8 має ранг 2 і т.д., а сума рангів складає 55, то ваговий коефіцієнт для мети 3 буде найбільшим і сума ваг усіх десяти цілей складе 1.
Вагу цілі доведеться визначати як:
(11 - 1) / 55 для цілі 3;
(11 - 2) / 55 для цілі 8 і т.д.
Під час використання групової експертної оцінки можна не тільки з’ясовувати думку експертів щодо показників, необхідних для системного аналізу. Дуже часто в подібних ситуаціях використовують так званий метод Дельфи (від легенди про дельфійського оракула). За ним опитування експертів проводять у кілька етапів, як правило – анонімно. Після чергового етапу від експерта потрібно не просто ранжирування, але й її обґрунтування. Ці обґрунтування повідомляються усім експертам перед черговим етапом без вказування авторів обґрунтувань. Наявний досвід свідчить про можливість істотно підвищити показовість, обґрунтованість і, головне, вірогідність суджень експертів. Як «побічний ефект» можна скласти думку про професійність кожного експерта.