3.1 Основні поняття математичної статистики
Розглянемо випадкові події і величини та їх основні характеристики. Як уже говорилося, під час аналізу великих систем наповнювачем каналів зв’язку між елементами, підсистемами і системи в цілому може бути:
— продукція, тобто реальні, фізично відчутні предмети із заздалегідь заданим способом їх кількісного і якісного опису;
— гроші, з єдиним способом опису – сумою;
— інформація, у вигляді повідомлень про події в системі і значеннях величин, що описують її поводження.
Почнемо з того, що звернемо увагу на тісний (системний) зв’язок показників продукції і грошей з інформацією про ці показники. Якщо розглядати деяку фізичну величину, скажімо – кількість проданих за день зразків продукції, то відомості про цю величину після продажу можуть бути отримані без проблем і досить точно або достовірно. Однак, зрозуміло, що під час аналізу нас куди більше цікавить майбутнє – а скільки цієї продукції буде продано за день? Це питання дуже важливе, оскільки нашою метою є керуваня, а образно висловлюючись, «керувати – значить передбачати».
Отже, без попередньої інформації, тобто, знань про кількісні показники в системі нам не обійтися. Величини, що можуть приймати різні значення залежно від зовнішніх щодо них умов, прийнято називати випадковими (стохастичними за природою). Так, наприклад, стать зустрінутої нами людини може бути жіночою або чоловічою (дискретна випадкова величина), причому, її зріст також може бути різним, але це вже неперервна випадкова величина з тією або іншою кількістю можливих значень (залежно від одиниці виміру).
Для випадкових величин (далі – ВВ) доводиться застосовувати статистичні методи їх опису. Залежно від типу самої ВВ – (дискретна або неперервна) це робиться по різному.
Дискретний опис полягає у тому, що вказуються всі можливі значення даної величини (наприклад – 7 кольорів звичайного спектра) і для кожної з них вказується ймовірність або частота спостережень саме цього значення для нескінченно великої кількості всіх спостережень. Можна довести (і це давно зроблено), що при збільшенні числа спостережень в певних умовах за значеннями деякої дискретної величини частота повторень даного значення буде усе більше наближатися до деякого фіксованого значення, яке і буде ймовірністю цього значення.
До поняття ймовірності значення дискретної ВВ можна підійти й іншим шляхом – через випадкові події. Це найпростіше поняття з теорії ймовірностей і математичної статистики – подія з ймовірністю «0.5» або 50% у 50 випадках зі 100 може відбутися або не відбутися, якщо ж її ймовірність більше «0.5» – вона частіше відбувається, аніж не відбувається. Події з ймовірністю «1» називають вирогідними, а з ймовірністю «0» – неможливими. Звідси просте правило: для випадкової події X сума ймовірностей P(X) (подія відбувається) і P(X) (подія не відбувається) для простої події дає «1».
Якщо ми спостерігаємо за деякою складною подією, наприклад, випаданням чисел 1..6 на верхній грані гральної кості, то можна вважати, що така подія має множину варіантів і для кожного з них ймовірність складає 1/6 за умови симетричності кості. Якщо ж кость несиметрична, то ймовірності окремих чисел будуть різними, однак їх сума буде дорівнювати 1. Однак, якщо розглядати результат кидання кості як дискретну випадкову величину, то прийдемо до поняття розподілу ймовірностей такої величини.
Нехай у результаті досить великого числа спостережень за гранню однієї і тієї ж кості ми отримали дані (табл. 3.1).
| Грані | 1 | 2 | 3 | 4 | 5 | 6 | Разом |
|---|---|---|---|---|---|---|---|
| Спостереження | 140 | 80 | 200 | 400 | 100 | 80 | 1000 |
Подібну таблицю спостережень за ВВ часто називають вибірковим розподілом, а відповідну їй діаграму – гістограмою (рис.3.1).
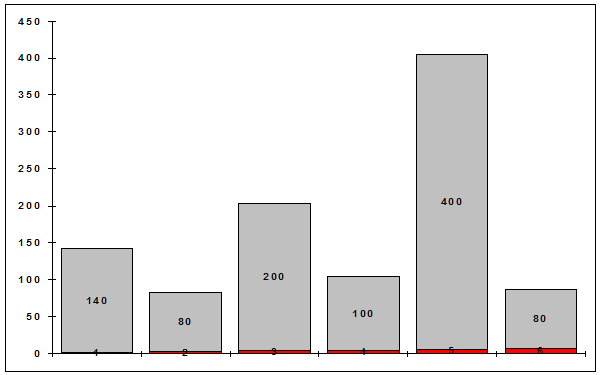
Яку ж інформацію несе така таблиця або відповідна їй гістограма?
Насамперед, всю – оскільки іноді і таких даних про значення випадкової величини немає і їх доводиться або діставати (експеримент, моделювання), або вважати результати такої складної події рівноможливими – по 1/6 для кожного з варіантів.
З іншого боку інформації дуже мало, особливо в цифровому, чисельному описі лише самої ВВ. Як, наприклад, відповісти на запитання: – а скільки в середньому ми виграємо за одне кидання кості, якщо виграш відповідає числу, що випало, на грані? Неважко підрахувати:
1*0.140+2*0.080+3*0.200+4*0.400+5*0.100+6*0.080 = 3.48
Те, що ми обчислили, називається середнім значенням випадкової величини, якщо нас цікавить минуле. Якщо ж ми поставимо питання інакше, тобто оцінити за цими даними наш майбутній виграш, то відповідь 3.48 прийнято називати математичним сподіванням випадкової величини, що у загальному випадку визначається як
Mx = ΣXi×P(Xi), (3.1)
де P(Xi) – ймовірність того, що X прийме своє i-те чергове значення.
Таким чином, математичне сподівання випадкової величини (як дискретної, так і неперервної) – це те, до чого прямує її середнє значення для досить великої кількості спостережень. Звертаючись до нашого прикладу, можна помітити, що кость несиметрична, інакше ймовірності складали б по 1/6 кожна, а середнє і математичне сподівання склало б 3.5. Тому доречне таке запитання – а яка ступінь асиметрії кості, і – як її оцінити за підсумками спостережень? Для цієї мети використовується спеціальна величина – міра розсіювання – так само як ми «усереднювали» допустимі значення ВВ, можна усереднити її відхилення від середнього. Але оскільки різниці (Xi – Mx) завжди будуть компенсувати одина одну, то доводиться усереднювати не відхилення від середнього, а квадрати цих відхилень. Величину прийнято називати дисперсією випадкової величини X:
(3.2)
Виконаємо таке обчислення для ВВ з розподілом за рис. 3.1.
| Грані (X) | 1 | 2 | 3 | 4 | 5 | 6 | Разом |
|---|---|---|---|---|---|---|---|
| X2 | 1 | 4 | 9 | 16 | 25 | 36 | |
| Pi | 0.140 | 0.080 | 0.200 | 0.400 | 0.100 | 0.080 | 1.00 |
| PiX21000 | 140 | 320 | 1800 | 6400 | 2500 | 2880 | 14040 |
Таким чином, дисперсія складе 14.04 – (3.48)2 = 1.930.
Зазначимо, що величина дисперсії не збігається з величиною самої ВВ і це не дозволяє оцінити величину розкиду. Тому найчастіше замість дисперсії використовується квадратний корінь з її значення – середньоквадратичне відхилення або відхилення від середнього значення:
складає в нашому випадку . Багато це або мало?
Відзначимо, що у випадку спостереження тільки одного з можливих значень (розкиду немає) середнє дорівнювало б саме цьому значенню, а дисперсія склала б 0. І навпаки – якби всі значення спостерігалися однаково часто (були б рівноможливими), то середнє значення склало б
(1+2+3+4+5+6)/6=3.500,
середнений квадрат відхилення визначиться як
(1+4+9+16+25+36)/6=15.167,
а дисперсія –як 15.167 – 13.25 = 3.917.
Таким чином, найбільше розсіювання значень ВВ має місце при її рівноможливому або рівномірному розподілі.
Слід відзначити, що значення Mx і Sx є розмірними і їх абсолютні значеннями мало про що говорять. Тому, часто для грубої оцінки "випадковості" даної ВВ використовують коефіцієнт варіації або відношення кореня квадратного з дисперсії до величини математичного сподівання:
у нашому прикладі ця величина складе 1.389/3.48 = 0.399.
Отже, запам’ятаємо, що невипадкова, тобто детермінована величина має математичне сподівання, що дорівнює їй самій, нульову дисперсію та нульовий коефіцієнт варіації, у той час як рівномірно розподілена ВВ має максимальну дисперсію і максимальний коефіцієнт варіації.
У багатьох ситуаціях доводиться мати справу з неперервно-розподіленими ВВ – вагами, відстанями і т.п. Для таких величин ідея оцінки середнього значення (математичного сподівання) і міри розсіювання (дисперсії) залишається тією ж, що і для дискретних ВВ. Доводиться тільки замість відповідних сум обчислювати інтеграли.
Другою відмінністю для неперервних ВВ є те, що питання про те, яка ймовірність прийняття нею конкретного значення, зазвичай не має сенсу, тобто, як перевірити, що вага товару складає точно 242 кг – і не більше і не менше (визначити точно неможливо)?
Для усіх ВВ – як дискретних так і неперервно розподілених, має велике значення питання про діапазон їх значень. І справді, іноді знання ймовірності події, що випадкова величина не перевищить задану границю, є єдиним способом використовувати наявну інформацію для системного аналізу і системного підходу щодо задачі керування системою. При цьому, правило визначення ймовірності влучення у необхідний діапазон, дуже просте – потрібно додати ймовірності окремих дискретних значень діапазону або проінтегрувати криву розподілу на цьому діапазоні.
Розглянемо взаємозв’язки випадкових подій. Звернемося знову до поняття випадкових подій і розглянемо спочатку прості події (може відбутися або ні). Ймовірність події Х позначимо через Р(Х) і розумітимемо, що ймовірність того, що подія не відбудеться, складає:
P(X) = 1 – P(X), (3.5)
Найважливішим під час розгляду декількох випадкових подій (тим більше в складних системах з розвиненими зв’язками між елементами і підсистемами) – є розуміння способу визначення ймовірності одночасного настання декількох подій або – суміснення подій.
Розглянемо найпростіший приклад двох подій X і Y, ймовірності яких складають P(X) і P(Y). Тут важливе лише одне питання – ці події незалежні або навпаки взаємозалежні, що приводить до ще одного питання – яка міра зв’язку між ними? Спробуємо розібратися в цьому питанні.
Оцінимо спочатку ймовірність одночасного настання двох незалежних подій. Елементарні міркування приведуть нас до висновку: якщо події незалежні, то при 80%-й ймовірності X і 20%-й ймовірності Y одночасне їх настання має ймовірність усього лише 0.8 ∙ 0.2 = 0.16, тобто 16%. Отже – ймовірність настання двох незалежних подій визначається добутком їх ймовірностей:
P(XY) = P(X)×P(Y), (3.6)
Перейдемо тепер до залежних подій. Назвемо ймовірність події X за умови, що подія Y уже відбулася умовною ймовірністю P(X/Y), вважаючи, при цьому, P(X) безумовною або повною ймовірністю. Такі ж прості міркування приводять до так званої формули Байєса:
P(X/Y)×P(Y) = P(Y/X)×P(X), (3.7)
де у лівій і правій частині записані ймовірності одночасного настання двох «залежних» або корельованних подій.
Доповнимо цю формулу загальним виразом, що описує безумовну ймовірності події X:
P(X) = P(X/Y)×P(Y) + P(X/Y)×P(Y), (3.8)
яка означає, що подія X може відбутися або після того як подія Y відбулася, або після того, як вона не відбулася (Y) – третього не може бути!
Формули Байєса (байєсівський підхід) до оцінки ймовірнісних зв’язків для простих подій і дискретно розподілених ВВ відіграють вирішальну роль у теорії прийняття рішень в умовах невизначеності, наслідків цих рішень, або в умовах протидії з боку природи, або у інших великих систем (конкуренції). За цих умов ключовою буде стратегія керування, що заснована на прогнозі апостеріорної (після дослідної) ймовірності події
, (3.9)
Насамперед, ще раз відзначимо взаємний зв’язок подій X і Y, і якщо одна не залежить від іншої, то вищенаведений вираз перетвориться на тривіальну тотожність. До речі, ця обставина використовується під час розв’язання задач оцінки тісноти зв’язків, тобто під час кореляційного аналізу. Якщо ж взаємозв’язок подій має місце, то формула Байєса дозволяє вести керування шляхом оцінки ймовірності досягнення деякої мети на основі спостережень над процесом функціонування системи, тобто, шляхом перерахунку варіантів стратегій з урахуванням уявлень, що змінились, тобто нових значень ймовірностей. Справа у тому, що будь-яка стратегія керування буде будуватися на базі визначених уявлень про ймовірність подій у системі і на перших кроках ці ймовірності будуть узяті «з голови» або у кращому випадку з досвіду керування іншими системами. Однак, впродовж «життя» системи не можна відкидати можливість керування, тобто, використання всього здобутого дотепер досвіду.