3.5 Лінійна регресія
У тих випадках, коли з природи процесів у системі або з даних спостережень над нею випливає висновок про нормальний закон розподілу двох ВВ – X і Y, з яких одна є незалежною, тобто Y є функцією від X, то виникає спокуса визначити таку залежність «формульно», аналітично. При цьому, було б набагато простіше вести системний аналіз – особливо для елементів системи типу «вхід-вихід». Звичайно, найпривабливішою є лінійна залежність типу Y = a + bX. Подібна задача є задачею регресійного аналізу і має такий спосіб розв’язання. Висувається така гіпотеза:
H0 : випадкова величина Y для фіксованого значення величини X розподілена за нормальним законом з математичним сподіванням:
My = a + bX,(3.14)
і дисперсією Dy, що не залежить від X.
За наявності результатів спостережень над парами Xi і Yi попередньо обчислюються середні значення My і Mx, а потім здійснюється оцінка коефіцієнта b у вигляді:
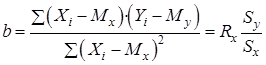, (3.15)
що випливає з визначення коефіцієнта кореляції за (3.1). Після цього обчислюється оцінка для a у вигляді:
a = My – b×Mх,(3.16)
і здійснюється перевірка значимості отриманих результатів. Таким чином, регресійний аналіз є потужним, хоча і, далеко, не завжди доступним розширенням кореляційного аналізу, розв’язуючи усе ту ж задачу оцінки зв’язків у складній системі.