СИСТЕМНИЙ АНАЛІЗ

3.6 Елементи теорії статистичних рішень

Що таке – статистичне рішення? Як найпростіший приклад розглянемо ситуацію, у якій треба зіграти у таку гру:

• вам заплатять 2 долари, якщо підкинута монета впаде догори гербом;
• ви заплатите 1 долар, якщо вона впаде гербом униз.

Швидше за все, ви погодитеся зіграти, хоча розумієте степінь ризику. Ви усвідомлюєте, «знаєте» про рівно ймовірнісні появи герба і «обчислюєте» свій виграш 0.5∙2 – 0.5∙1 = +$0.5.

Ускладнимо цю гру. Ви бачите, що монета трохи вигнута і можливо буде падати частіше однією зі сторін. Тепер рішення грати або не грати як і раніше залежить від ймовірності виграшу, що не може бути заздалегідь (по-латинському – apriori) прийнятою рівною 0.5.

Людина, що знайома із статистикою, спробує оцінити цю ймовірність за допомогою дослідів, якщо, зазвичай, вони можливі і коштують не дуже дорого. Звідси виникає питання – скільки таких підкидань вам буде досить?

Нехай ви платите 5 центів за одне експериментальне кидання, а ставки у грі складають $2000 проти $1000. Швидше за все, ви погодитесь грати, заплативши порівняно невелику суму за 100..200 експериментальних кидків. Ви, напевно, будете вести підрахунок вдалих падінь і, якщо їх число складе 20 з 100, припините експеримент і зіграєте на ставку $2000 проти $1000, оскільки очікуваний виграш оцінюється у 0.8∙2000 + 0.2∙1000 – 100∙0.05 = $1795.

У наведених прикладах головним для прийняття рішення була ймовірність успішного результату падіння монети. У першому випадку – апріорна ймовірність, а у другому – апостеріорна. Таку інформацію прийнято називати даними про стан природи.

Наведені приклади мають безпосереднє відношення до сутності нашого предмета. І справді – під час системного керування доводиться приймати рішення в умовах, коли наслідки таких рішень заздалегідь вірогідно невідомі. При цьому питання: грати або не грати – не стоїть! «Грати» треба, тобто, треба керувати системою. Ви запитаєте – а як же заборона на експеримент­ти? Відповідь можна дати таку – сама поведінка системи у звичайному її ста­ні може розглядатися як експеримент, з якого для правильної організації збору та обробки інформації про поведінку системи можна чекати на одержання даних для з’ясування особливості системного підходу до розв’язання задач керування.

Для детальнішого розуміння теорії статистичних рішень розглянемо такий приклад. Нехай для характеристики об’єктів використовується ознака х, а уся їх сукупність розбита на два класи Ω₁ і Ω₂. При цьому, вважа­тимемо, що відомі описи цих класів, тобто відомі умовні щільності розподілу ймовірностей f₁(x) і f₂(x) значень ознаки об’єктів класів Ω₁ і Ω₂, а також апріорні ймовірності P(Ω₁) і P(Ω₂) появи об’єктів.

Нехай за результатами експерименту визначено значення ознаки х⁰ досліджуваного об’єкта (рис. 3.2).

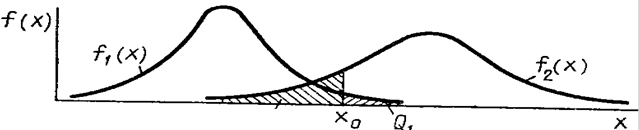
Щоб прийняти рішення до якого класу віднести досліджуваний об’єкт, позначимо через х⁰ деяке доки ще невизначене значення ознаки х₀, і домовимося про таке правило. Якщо значення ознаки задовольняє умові х⁰ > х₀, то об’єкт відносимо до класу Ω₂, а якщо задовольняється умова x⁰ ≤ х₀, то до класу Ω₁.

При цьому, якщо об’єкт відноситься до класу Ω₁, а його вважають об’єктом класу Ω₂, то це свідчить про помилку прийняття рішення – помилка першого роду, умовна ймовірність якої визначається за виразом:

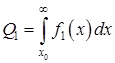, (3.17)

Відповідно термінології теорії статистичних рішень у цьому випадку помилково вибрана гіпотеза H₂, у той час коли вірною є гіпотеза Н₁. І навпаки, коли вірною є гіпотеза Н₂, а віддана перевага гіпотезі H₁, то вчинена помилка другого роду, умовна ймовірність якої визначається як:

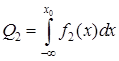,(3.18)

Умовні ймовірності правильних рішень для випадків справедливості гіпотез H₁ і H₂ визначаються відповідно як:

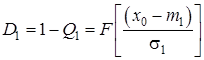,(3.19)

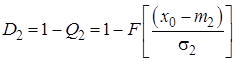,(3.20)

де D₁ – визначає розмірність іспитів,

D₂ – їх потужність.

Міркування, якими слід керуватися під час вибору значення ознаки х₀ (розбиття простору ознаки х на півпростори R₁ і R₂) повинні враховувати втрати, що пов’язані з правильними і помилковими рішеннями. Ці втрати зазвичай описують у вигляді платіжної матриці:

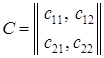,(3.21)

де с₁₁ і с₂₂, с₁₂ і с₂₁ – втрати, що пов’язані відповідно з правильними рішеннями і помилками першого і другого виду.

При цьому, у випадку багатократного застосування задачі прийняття рішень, середній ризик буде дорівнювати сумі втрат, що пов’язані з неправильними і правильними рішеннями, з урахуванням ймовірностей їх появи і апріорних ймовірностей появи об’єктів класів Ω₁ і Ω₂.

.(3.22)

Підставляючи у (3.22) вирази (3.19) і (3.20), отримаємо:

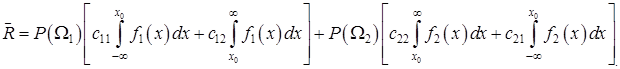.(3.23)

Оскільки прийняття рішень практично завжди є задачею багатократного застосування, значення х₀ слід вибирати таким чином, щоб значення середнього ризику було мінімальним. Щоб визначити значення х₀ , для якого середній ризик буде мінімальним, знайдемо його диференціал по х і прирівняємо отриману похідну до нуля, поклавши що х = х₀.

,(3.24)

звідки можна записати, що:

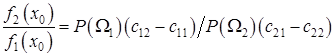.(3.25)

Відношення умовних щільностей розподілу f₂(x)/f₁(x) = l(х) називають коефіцієнтом або відношенням правдоподібності. При цьому, права частина виразу (3.25).

,(3.26)

визначає порогове (критичне) значення коефіцієнту правдоподібності.

Значення х₀ дозволяє оптимальним чином (з точки зору мінімуму середнього ризику) розбити простір значень ознаки х на області R₁ і R₃. Область R₁ включає значення х ≤ х₀, для яких λ(x) ≤ λ₀, а область R₂ – значення х > х₀, для яких λ(x) > λ₀. Тому, рішення про віднесення досліджуваного об’єкта до класу Ω₁ слід приймати, якщо значення коефіцієнта правдоподібності менше або дорівнює його критичному значенню. Інакше, об’єкт слід віднести до класу Ω_3.

У загальному випадку, коли число класів m > 2, а об’єкти описуються набором ознак x_i,..., х_N або вектором x = {x_i, ..., х_N}, відношення правдоподібності між класами Ω_k і Ω_l буде визначатися як:

λ_kl = f_k(х) / f_l(х),    k,l = 1, ..., m,(3.27)

платіжна матриця має вигляд:

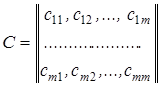,(3.28)

а середній ризик обчислюється за виразом:

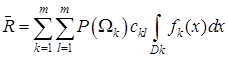,(3.29)

З умови мінімуму значення середнього ризику рівняння границь у багатомірному просторі ознак між областями D_k і D_l, що відповідають класам Ω_k і Ω_l, буде визначатися як:

, (3.30)

При цьому, якщо покласти, що c_kk = c_ll = 0, a c_kl = c_lk = 1, то будемо мати:

P(Ω_k) f_k(x) – P(Ω_l) f_l(x) = 0,(3.31)

log P(Ω_k) f_k(x) / [P(Ω_l) f_l(x)] = 0.(3.32)