3.7 Критерій Байєса
Критерій Байєса – правило, за яким стратегія прийняття рішень вибирається таким чином, щоб забезпечити мінімум середнього ризику. Застосування критерію Байєса доцільне для систем багатократного розпізнання в умовах незмінного простору ознак, незмінного опису класів і незмінній платіжній матриці.
З теорії статистичних рішеньвідомо, що мінімум середнього ризику, забезпечується тільки тоді, коли рішення про віднесення об’єктів до класів Ω1 або Ω2 приймаються за правилом: якщо виміряне значення ознаки об’єкта знаходиться в області R1, то об’єкт відносять до класу Ω1, а якщо це значення знаходиться в області R2 – до класу Ω3.
Стратегію і мінімальний середній ризик, щл визначаються за таким правилом, називають байєсівськими.
Байєсівска стратегія може бути описана також і таким чином. Нехай за результатами дослідів встановлено, що значення ознаки об’єкта визначається як х = х0. Тоді умовна ймовірність приналежності об’єкта до класу W1 (умовна ймовірність першої гіпотези) відповідно з теоремою гіпотез або формулою Байєса визначиться як:
,(3.33)
а умовна ймовірність приналежності об’єкта класу Ω2 (умовна ймовірність другий гіпотези) – як:
,(3.34)
де f(x0) = P(Ω1) f1(x0) + P(Ω2) f2(x0) – спільна щільність розподілу ймовірностей значень ознаки х по класах;
P(Ω1 | х0) і Р(Ω2 | х0) – апостеріорні ймовірності того, що досліджуваний об’єкт належить класам Ω1 і Ω2 відповідно.
При цьому, умовні ризики, що пов’язані з рішеннями ω ∈ Ω1 і ω ∈ Ω2, будуть визначатися відповідно як:
(3.35)
Система розпізнання за байєсівською стратегією повинна розв’язувати задачу з мінімальним умовним ризиком. Це означає, що перевагу рішенню ω ∈ Ω1 слід віддавати тільки тоді, коли виконується умова:
[R(Ω1 | x0) / R(Ω2 | x0)] < 1.(3.36)
Підставимо у цей вираз значення R(Ω1 | x0) і R(Ω2x0), що визначені за (3.35). Тоді нерівності:
c1R(Ω1 | x0) > c2R(Ω2 | x0),(3.37)
або
[R(Ω1 | x0) / R(Ω2 | x0)] > c2 / c1,(3.38)
будуть визначати умови, за якими слід приймати рішення що ω ∈ Ω1.
Таким чином, байєсівський підхід до розв’язання задачі прийняття рішення полягає в обчисленні умовних апостеріорних ймовірностей і порівняння їх значень. Саме це і забезпечує мінімум середнього ризику, а значить і помилкових рішень. Узагальнюючи вищеописане для число варіантів рішень m > 2, апостеріорна ймовірність віднесення об’єкта до класу Ωі буде визначатися як:
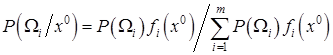.(3.39)
При цьому, якщо об’єкт або система до того ж характеризується ознаками xj, j = 1, N, і ці ознаки прийняли значення х1=х10, х2=х20, ..., хN=хN0, ймовірність того, що за умови появи події An = (x10, х20, ..., xN0), об’єкт відноситься до i-го класу дорівнює:
P(Ωi | AN) = [P(Ωi)fi(x10,x20,...,xn0)] / Sm P(Ωi)fi(x10,x20,...,xn0),(3.40)
Розглянемо ще одну форму запису байесівського критерію віднесення об’єкту до відповідного класу. Нехай є класи Ω1 і Ω2 . Апріорні ймовірності появи об’єктів цих класів будуть відповідно P(Ω1) і P(Ω2), с11=с22=0, с12=с1 і с21=с3. Відомі також багатомірні умовні щільності розподілу ймовірностей значень ознак f1(x1,...,хn) і f2(х1,...,хn) по класам. Тоді умовні ймовірності помилок першого і другого роду будуть визначатися відповідно як:
Q1 = ∫R3...∫f1(x1,...,xn)dx1,...,dxn, Q2 = ∫R1...∫f2(x1,...,xn)dx1,...,dxn,(3.41)
Середній ризик, при цьому буде визначатись за виразом:
R = c1P(Ω1)Q1 + c2P(Ω2)Q2,(3.42)
Оскільки інтеграл від щільності розподілу ймовірності по областях R1 і R2 дорівнює одиниці, то Q1 = 1 – ∫...∫f1(x1...xn)dx1....dxn, звідки:
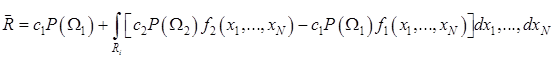,(3.43)
Задача полягає у тому, щоб мінімізувати значення середнього ризику. Для цього необхідно так вибрати області Ri і Рч, щоб інтеграл у (3.43) прийняв найбільше від’ємне значення. Це досягається тоді, коли вираз під інтегралом приймає найбільше від’ємне значення і поза областю Ri не існує такої області, де вираз під інтегралом буде від’ємним, тобто:
c2P(Ω2) f2(x1, ..., хN) – c1P(Ω1) f1(x1, ..., хN) < 0,(3.44)
Звідси випливає вже відоме правило прийняття рішень. Досліджуваний об’єкт, ознаки якого, як встановлено за результатами експерименту, дорівнюють х1 = х10, x2 = х20, ..., хn = хn0, то відноситься до класу Ω1, якщо:
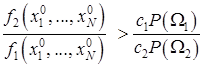,(3.45)
де c1Р(Ω1)/с2P(Ω2) = λo – порогове значення коефіцієнта правдоподібності.