3.8 Мінімаксний критерій
На практиці можливі такі ситуації, коли апріорні ймовірності появи об’єктів відповідних класів невідомі. У цьому випадку мінімізувати значення середнього ризику прийняття рішень за байєсівською стратегією не вдається. У цій ситуації доцільно використовувати критерій, що мінімізує максимально можливе значення середнього ризику (мінімаксним критерій).
Мінімаксна стратегія полягає у тому, що рішення про приналежність об’єкта відповідному класу приймається на основі байєсівської стратегії, що відповідає такому значенню P(Ωi), для якого середній ризик буде максимальним. Покажемо перевагу мінімаксної стратегії у порівнянні з іншими в умовах коли невідомі значення P(Ωі), і=1,...,m.
За наявності класів Ω1 і Ω2 байєсівський ризик з урахуванням того, що Р(Ω2) = 1 – P(Ω1), с11=с22 = 0, a c12 = с1 і с12с2, рівні:
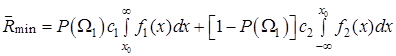,(3.46)
Побудуємо графік функції Rmin = f [P(Ω1], пам’ятаючи при цьому, що для P(Ω1) = 0 і P(Ω1) = 1 Rmin = 0 (рис. 3.3).
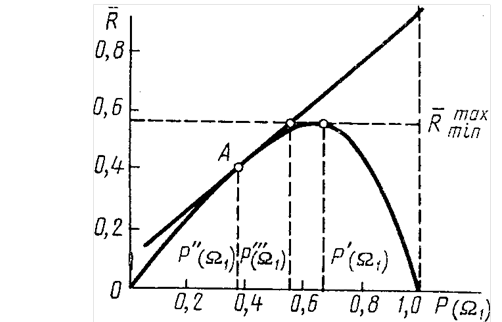
Нехай Rmin досягає свого найбільшого значення при P(Ω1) = P’(Ω1). Цей ризик дає максимальне значення мінімального байєсівського ризику (позначимо його як Rminmax). Застосування мінімаксного критерію означає, що за відсутності даних щодо апріорних ймовірностей появи об’єктів слід орієнтуватися на P(Ω1) = P’(1), середні втрати при чому визначаються дотичною до кривої R = f[P(1)] у точці P’(Ω1).
Для визначення алгоритму прийняття рішення відповідно мінімаксній стратегії, продиференціюємо (3.46) по P(Ω1) і прирівняємо цю похідну до нуля. У результаті отримаємо:
c1Q1(x0) = c2Q2(x0),(3.47)
Це співвідношення, що описує рівність умовних значень середніх ризиків при помилках першого і другогороду, дозволяє визначити х0 і побудувати такий алгоритм класифікації. Якщо значення ознаки х об’єкта ω дорівнює х0, то ω ∈ Ω1 якщо х = х0є х0, і ω ∈ Ω2 якщо х = х0 > х0.
Минимаксна стратегія, що пропонує значення P(Ω1>) = P’(1), дає порогове значення коефіцієнту правдоподібності:
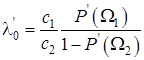,(3.48)
Визначення λ`0 дозволяє записати алгоритм класифікації у вигляді: ω ∈ Ω1 якщо λ(x) ≤ λ`0 і ω ∈ Ω2, якщо λ(x) >λ`0. При цьому, якщо с1=с2, то мінімаксна стратегія призводить до рівності умовних ймовірностей помилок першого і другого роду.
На завершення відзначимо, що мінімаксна стратегія є байесівською стратегія для найгірших значень апріорних ймовірностей, що дасть хоча і обережне, але гарантоване значення середнього ризику.