СИСТЕМНИЙ АНАЛІЗ

3.9 Критерій Неймана-Пірсона

На практиці часто буває, що можуть бути невідомі не тільки апріорні ймовірності появи об’єктів відповідних класів, але й платіжні матриці. У таких системах для побудови алгоритму класифікації доцільно скористатися критерієм Неймана-Пірсона, суть якого полягає у такому.

Виходячи з того, що рішення приймаються за результатами експерименту над об’єктами, визначається допустиме (задане) значення умовної ймовірності помилки першого роду, а після цього визначається така границя між класами прийняття рішень, дотримуючись якої вдається досягти мінімуму умовної ймовірності помилки другого роду.

Нехай з деяких міркувань прийнято рішення, що допустима умовна ймовірність помилки першого виду не повинна перевищувати деякої постійної величини Q₁ ≤ A. Треба визначити х₀ для задачі minQ₂ = min f₂(x)dx за обмежень типу Q₁ = ∫f₂(x)dx ≤ А. Oчeвидно, що рішення x_о задовольняє рівнянню ∫f₁(x) dx = A, оскільки для значення х_о` > х_о умовна ймовірність помилок другого роду Q₂ зростає. Обрати ж значення x_о’ << х_о не можна за умовою задачі.

На завершення розглянемо геометричну інтерпретацію вищевказаних критеріїв. Для цього в координатах D_i = 1 – Q_i і Q_i побудуємо характеристику (рис. 3.4), відзначаючи що для Q₁ = 0 Q₂ = 1 і D₂ = 0, і навпаки, для Q₁ = l Q₂ = 0 і D₂ = l. Оскільки Q₁ = ∫ f₁(x)dx, a D₂ = ∫ f₂(x)dx, то продиференціювавши D₂ по Q₁, отримаємо, що:

, (3.49)

Однак, диференціал dD₂/dQ₁ ;є тангенсом кута нахилу дотичної до робочої характеристики для λ = λ_о. Тому, для визначення Q₁ і D₁ на основі застосування критерію Байеса на робочій характеристиці знайдемо точку, дотична у якій має нахил, що дорівнює λ_о = [Р(Ω₁)с₁/Р(Ω₂)с₂], тобто tg α = λ_o. Тепер ордината цієї точки визначає умовну ймовірність правильного рішення, а абсциса – означає умовну ймовірність помилки першого роду.

Для визначення Q₁ і D₂ за мінімаксним критерієм необхідно враховувати, що похідна від середнього ризику за апріорною ймовірністю P(Ω₁) у точці його максимуму дорівнює нулю. Оскільки:

R = c₁₁P(Ω₁) (l – Q₁) + с₁₂P(Ω₁)Q₁ + с₂₂[1 – P(Ω₁)]D₂ + c₂₁[l – P(Ω₁)](1 – D₂),(3.50)

тo

∂R/∂P(Ω₁) = c₁₁(1 – Q_l) + c₁₂Q₁ – c₂₂D₂ – c₂₁(1D₂) = 0.(3.51)

В координатах Q₁ і Q₂ це рівняння прямої і якщо с₁₁ = с₂₂, то:

D₂ = Q₁[c₁₁ - c₁₂)/(c₂₁ - c₂₂)]+1,(3.52)

з кутовім коефіцієнтом γ = tgβ = [(c₁₁ – с₁₂)/(c₂₁ – с₂₂)] + 1.

Проведемо на графіку (рис. 3.4) цю пряму АВ.

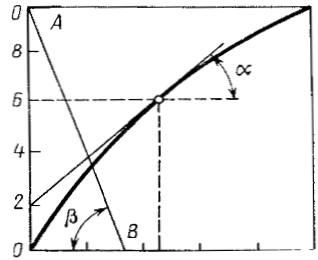
Координати точки перетину цієї прямої з робочою характеристикою визначають умовні ймовірності Q₁ і D₂ = 1 – Q₂ в умовах застосування мінімаксного критерію. Тангенс кута нахилу дотичної у цій точці дорівнює λ_о.