1.3. Відношення. Пропорція. Властивості пропорції

Відношенням числа а до числа b називається частка чисел а і b, тобто а/b (або а:b).

Пропорцією називається рівність двох відношень, тобто 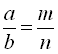; а і п називають крайніми членами пропорції, b і т – середніми членами пропорції.

Властивості пропорції

1) Добуток крайніх членів пропорції дорівнює добутку її середніх членів, тобто якщо , то .

2) Із пропорції випливають такі пропорції , , тобто в пропорції можна змінювати місцями крайні і середні члени або ті й інші одночасно.

3) Щоб знайти невідомий крайній (середній) член пропорції, треба добуток середніх (крайніх) членів поділити на відомий крайній (середній) член пропорції: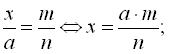

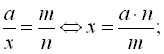
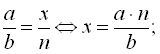
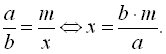
Наприклад: =;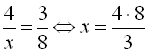

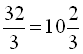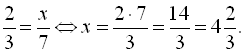
Певна кількість алгебраїчних задач розв’язується за допомогою пропорцій. Наведемо одну з таких задач.

Задача. У 800 грамах розчину міститься 50 грамів солі. Скільки солі міститься у 240 грамах розчину?

Розв’язання

Нехай 800 г розчину – це 50 г солі, а 240 г розчину – це х г солі. Складемо і розв’яжемо таку пропорцію: 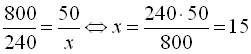. Отже, 15 грамів солі міститься у 240 грамах розчину.

Відповідь: 15 г.

1.4. Відсотки

Відсотком називається сота частина якого-небудь числа. Відсоток позначається знаком «%». Якщо дане число взяти за одиницю, то 1% складає 0,01 цього числа, 10% складають 0,1 числа, 25% відсотків складають 0,25 числа (або ? числа), 50% складають 0,5 числа (або ? числа), 75% складають 0,75 числа (або ? числа) і т.д. Щоб число відсотків виразити у вигляді дробу, треба число відсотків поділити на 100. Наприклад, 6%=0,06; 150%=1,5; 0,4%=0,004.

Правило 1. Щоб знайти р% від числа а, потрібно а помножити на р/100.

Правило 2. Якщо р% від числа с дорівнює а, то число 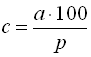. Правило 3. Відсоткове відношення чисел а і с дорівнює 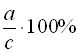. Задача 1. Знайти 40% від числа 80.

Розв’язання

40% від 80 знайдемо за правилом 1:

Задача 2. Хлопці у класі складають 75% від усієї кількості учнів. Дівчат у класі 8. Скільки всього учнів у класі?

Розв’язання

За умовою задачі хлопців у класі – 75%, тоді дівчат – 25%. Скористаємось правилом 2 для обчислення кількості учнів у класі: .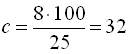

Відповідь: 32 учні.

Задача 3. Який відсоток становить число 28 від числа 35?

Розв’язання

За правилом 3 відсоткове відношення чисел 28 і 35 дорівнює .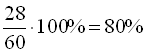

Всі 3 типи вищевказаних задач можна розв’язувати за допомогою пропорцій. Так, наприклад, задачу 2 можна було б розв’язати таким чином.

Якщо дівчат у класі 8 і це складає 25% всієї кількості, то нехай хлопців – х, що становить 75%. Складемо і розв’яжемо пропорцію: 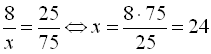. Отже, у класі 24 хлопці, тоді усіх учнів 24+8=32.

Відповідь: 32 учні.

Задача 4. Скільки кілограмів води варто додати до 7,5 кг 12%-го розчину солі, щоб одержати 10% розчин?

Розв’язання

Дізнаємось спочатку, скільки кілограмів солі міститься у 12% розчині. Для цього візьмемо масу 12%-го розчину 7,5 кг за 100%, масу солі в 12% – за х, тобто

7,5 кг – 100% або .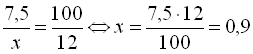

х кг – 12%

Отже, 0,9 кг солі міститься у 12% розчині солі.

Маса солі у новому розчині не змінилась, а змінилась лише її відсоткова частка. Тобто 0,9 кг становить 10%. Натомість невідому масу нового розчину візьмемо за 100% і позначимо через y. Тобто y кг – 100%. Складемо і розв’яжемо пропорцію: 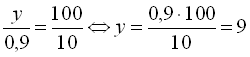. Тобто 9 кг – маса нового розчину. Звідси, долили води 1,5 кг (9 кг-7,5 кг).

Відповідь: 1,5 кілограма.

Якщо відомо, що р% числа х дорівнює а, то число х можна знайти за формулою . Наприклад, якщо 10% внеску в ощадбанк складають 250 доларів, то цей внесок дорівнює (доларів).

Якщо ставиться задача, що первісний внесок в ощадбанк дорівнює а доларів, за рік нараховується р відсотків, а потрібно обчислити суму внеску через п років, то використовуємо формулу складних відсотків: 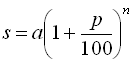, де s – величина внеску через п років.

Приклад: Первісний внесок в ощадбанк дорівнює 500 доларів, за рік нараховується 4%. Знайти суму внеску через 5 років.

Розв’язання

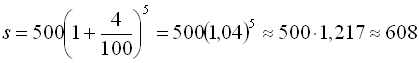(доларів).

Відповідь: 608 доларів.