1.5. Дії з алгебраїчними виразами
Алгебраїчні вирази – це математичні вирази, що складаються з чисел і змінних за допомогою знаків додавання, віднімання, множення, ділення, піднесення до раціонального степеня, добування кореня і за допомогою дужок. Множина значень змінних, при яких алгебраїчний вираз має значення, називається областю визначення алгебраїчного виразу. Наприклад, областю визначення виразу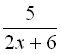 
є множина усіх значень 
, окрім 
. Областю визначення виразу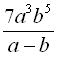 
є множина пар чисел 
, для яких 
.
В системі Maple операція піднесення до степеня задається символом ^ або послідовністю з двох зірочок (**).
Два вирази називаються тотожно рівними, якщо при всіх значеннях змінних, що входять до них і належать спільній області визначення, відповідні значення цих виразів рівні.
Тотожністю називається рівність, правильна при всіх припустимих значеннях змінних, що входять до неї. Приклади тотожностей: 
, 
, 
.
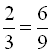Заміна одного виразу іншим, який тотожно дорівнює йому, називається тотожним перетворенням виразу.
Одночленом називають такий вираз, який містить числа, натуральні степені змінних та їх добуток, і не містить ніяких інших дій над числами і змінними.
Будь-який одночлен можна привести до стандартного вигляду, тобто записати у вигляді добутку числового множника, що стоїть на першому місці, та степенів різних змінних. Числовий множник одночлена, записаного в стандартному вигляді, називають коефіцієнтом одночлена. Суму показників степенів усіх змінних називають степенем одночлена.
Приведення одночлена до стандартного вигляду, множення одночленів – тотожні перетворення. Одночлени, приведені до стандартного вигляду, називаються подібними, якщо вони відрізняються тільки коефіцієнтом або зовсім не відрізняються. Подібні одночлени можна додавати і віднімати, в результаті чого знову отримують одночлен, подібний первинному (інколи отримують 0). Додавання і віднімання подібних одночленів називають зведенням подібних членів.
Многочленом називають суму одночленів. Якщо всі члени многочлена записати в стандартному вигляді і виконати зведення подібних членів, то отримаємо многочлен стандартного вигляду.
Щоб звести подібні члени (доданки), достатньо додати їх числові коефіцієнти і отримане число помножити на спільний буквений вираз. Наприклад, 
.
Подібні перетворення в системі Maple відбуваються автоматично
> (3*x^4-x)-(x^4+3*x)-(1-4*x);
Якщо ж маємо аналогічний вираз з нечисловими коефіцієнтами, то автоматичного спрощення не відбувається і в подібних випадках за допомого потрібно звертатись до одної із команд системи. В даному випадку потрібно звести подібні члени – за допомогою команди collect:
> (a[1]*x^4-x)-(a[2]*x^4+a[3]*x)-(1-a[4]*x);
collect(%,x);
Взагалі для алгебраїчних перетворень Maple має потужні вбудовані функції:
simplify – спростити, expand – розкрити дужки, factor – розкласти на множники, normal – звести до спільного знаменника, collect – звести подібні члени. Для позначення команд Maple підібрані англійські слова так, щоб було зрозумілим призначення команди. Зокрема, очевидно, що функція simplify призначена для спрощення виразу, який передається цій функції як параметр. Функція simplify, як і багато інших команд системи, має багато опцій, в залежності від яких підключаються одні або інші алгоритми для перетворення виразу. В посібнику наведено чисельні приклади використання команд перетворення. Слід зазначити, що термін «перетворення» є більш універсальним ніж термін «спрощення», адже в різних контекстах під спрощеним виразом можна розуміти альтернативні форми одного й того ж самого виразу.
В деяких випадках приведення цілого виразу до стандартного вигляду многочлена здійснюється за допомогою тотожностей:
;
;
;
;
;
;
.
Ці тотожності називають формулами скороченого множення.
Наведемо приклад розкриття дужок однієї з вищевказаних тотожностей в ситемі Maple:
> expand((a-b)*(a+b));
А тепер навпаки на множники розкладемо
> factor(a^3-b^3);
Розкладанням многочлена на множники називається перетворення многочлена в добуток двох або декількох многочленів, серед яких можуть бути і одночлени.
Способи розкладання многочлена на множники
1) Винесення спільного множника за дужку. Кожну змінну, яка входить у всі члени многочлена, виносять з найменшим показником, який вона має в даному многочлені: 
.
Приклад 1. 
> factor(10*x^2*y-5*x*y^3);
2) Використання формул скороченого множення.
Приклад 2. 
.
3) Спосіб групування. Він полягає у поєднанні в групи тих членів, які мають спільні множники, за дужки виноситься спільний множник кожної з груп. Якщо після такого перетворення виявиться спільний множник у всіх утворених групах, то його виносять за дужки.
Приклад 3. 
> factor(3*x^3-2*y^3-6*x^2*y^2+x*y);
Розкладання квадратного тричлена на лінійні множники
Якщо 
і 
– корені квадратного тричлена 
(тобто корені рівняння 
), то 
.
Приклад 4. 
, тому що 
.
Приклад 5.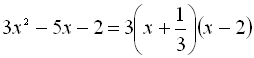 
, так як 
.
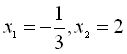Виділення повного квадрата двочлена з квадратного тричлена
Нехай є квадратний тричлен 
і потрібно перетворити його до виду 
Для цього чинимо в такий спосіб: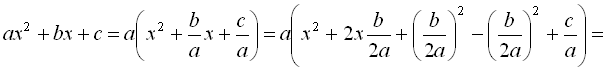 
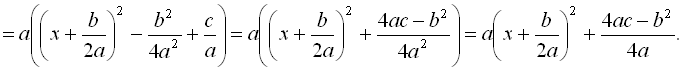Наведемо приклади на виділення повного квадрата.
Приклад 6. 
.
Приклад 7.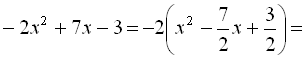 
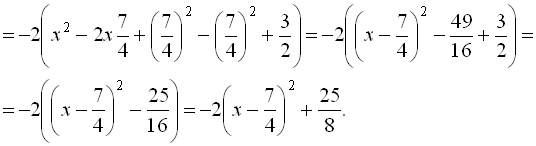
Система Maple має власну мову програмування. В багатьох випадках простіше скласти власну процедуру, аніж шукати відповідну стандартну функцію. Створимо та продемонструємо роботу функції, яка вилучає повний квадрат двочлена з квадратного тричлена:
> `Повн_квадрат`:=proc(`тричлен`,xn)
local L;
match(`тричлен` = A*x^2+B*x+C, xn, 'L');
A*(xn+B/2/A)^2+(4*A*C-B^2)/4/A;
subs(L,%);
end proc;
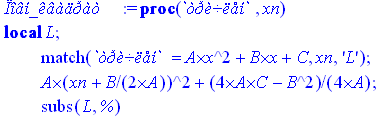
> `Повн_квадрат`(x^2-4*x+1,x);
> -2*x^2+7*x-3=`Повн_квадрат`(-2*x^2+7*x-3,x);
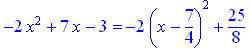
Перетворення цілих раціональних виразів зводиться до віднімання, додавання, множення та піднесення змінних до натурального степеня.
Приклад 8. Як записати вираз у вигляді добутку:
а) 
; б) 
.
Розв’язання
а) 
.
б) 
.
Перетворення дробових раціональних виразів зводиться до віднімання, додавання, множення та ділення раціональних дробів, а також до піднесення дробу до натурального степеня. Будь-який раціональний вираз можна перетворити в дріб, чисельник і знаменник якого – цілий раціональний вираз; в цьому, як правило, полягає мета тотожних перетворень раціональних виразів.
Приклад 9. Спростити вираз
.
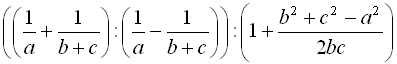Розв’язання
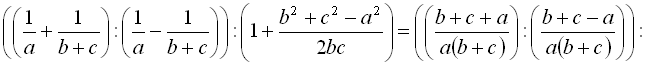
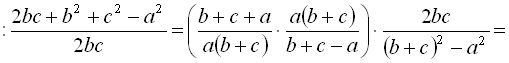
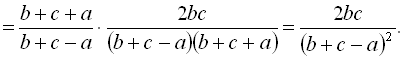
>simplify(((1/a+1/(b+c))/(1/a-1/(b+c)))/(1+(b^2+c^2-a^2)/(2*b*c)));
Одержаний в Maple вираз є тотожно рівним з тим, що ми отримали, розв’язуючи даний приклад «вручну».
Приклад 10. Спростити вираз
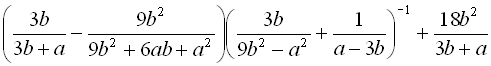
Розв’язання
1) 
;
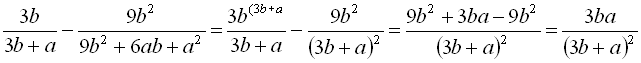2) 
;
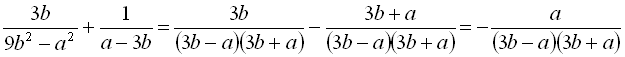Покажемо, як в системі Maple за допомогою команди normal звести вираз до спільного знаменника:
> normal(3*b/(9*b^2-a^2)+1/(a-3*b));
3) 
;
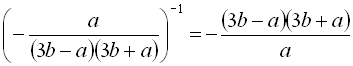4) 
;
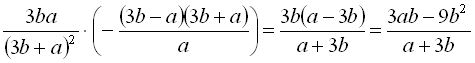5) 
.
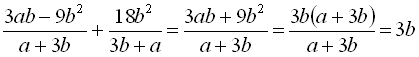Команда normal не тільки зводить вираз до спільного знаменника, а й виконує скорочення дробу. Покажемо це на дії 5) попереднього прикладу:
> normal((3*a*b-9*b^2)/(a+3*b)+18*b^2/(3*b+a));
Досвід показує, що для спрощення виразів потрібно користуватися різними командами. Розглянемо дріб
> p_27:=(x^27-1)/(x-1);
Застосування команд normal та simplify в даному випадку приводить до одного й того самого виразу
> p_27=normal(p_27);
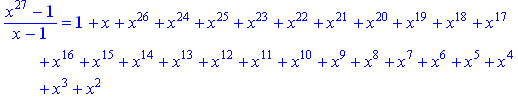
> p_27=simplify(p_27);
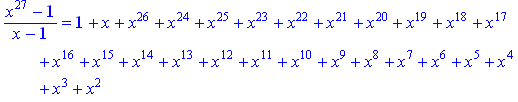
Застосування команди factor приводить до іншої форми того самого виразу
> p_27=factor(p_27);
Для того, щоб в Maple не займатися набором слів, які є найбільш використовуваними, існує Smart-спосіб з використанням контекстного меню. Робиться це так. Вводиться вираз і виводиться його математичний вид, який виділяється за допомогою миші. Після чого, коли СКМ знаходиться на ньому, клацаємо ПКМ – з’являється контекстне меню. Встановлюєте СКМ на потрібному ключовому слові і клацаєте ЛКМ, тоді відбувається виконання вибраної команди.
Наберемо вираз прикладу 10, виводиться його стандартний математичний вигляд, виділяється і відкривається контекстне меню. За командою simplify відбувається спрощення і в наступній секції з’являється результат.
Наберемо в командному рядку вираз прикладу 3 та натиснемо
>(3*b/(3*b+a)-9*b^2/(9*b^2+6*a*b+a^2))*(3*b/(9*b^2-a^2)+1/(a-3*b))^(-1)+18*b^2/(3*b+a);
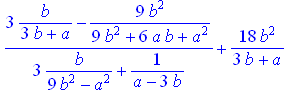
Наводимо СКМ на вираз, що з’явився в області виведення, клацаємо ПКМ та ЛКМ вибираємо потрібну команду, як показано на рис.
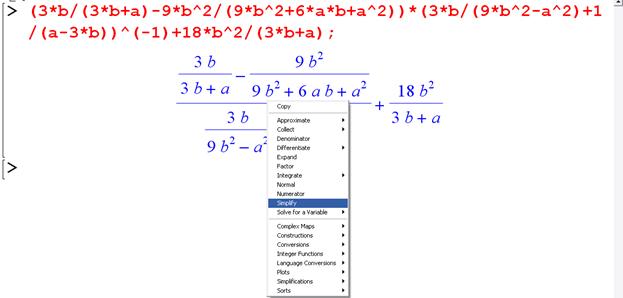
Результатом цих дій буде поява командного рядка та результат його виконання у вигляді спрощеного виразу
> R0:= simplify( (3*b/(3*b+a)-9*b^2/(9*b^2+6*a*b+a^2))/(3*b/(9*b^2-a^2)+1/(a-3*b))+18*b^2/(3*b+a) );
