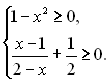3.3. Метод заміни змінної при розв’язанні раціональних нерівностей
Приклад 13. Розв’язати нерівність 
Розв’язання
Зробимо заміну 
, тоді 
. Розкладемо на множники квадратний тричлен, який стоїть у лівій частині нерівності: 
або 
.
Оскільки 
, то дістаємо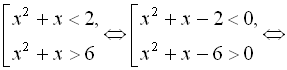 
.
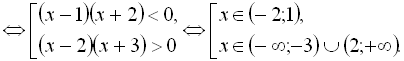
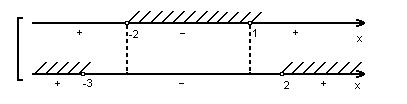
Відповідь: 
.
3.4. Тренувальні вправи
Рівень А
Розв’язати нерівності:1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
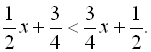
12. 
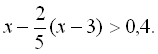
13. 
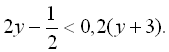
14. 
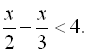
15. 
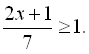
16. 
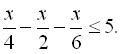
17. 
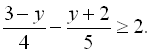
18. 
19. 
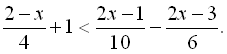
20. 
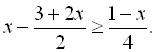
21. 
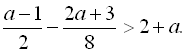
22. 
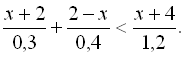
23. 
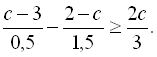
24. 
25. 
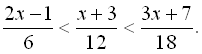
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Рівень Б
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
Розв’язати раціональні нерівності методом інтервалів:
Рівень А
1. 
2. 
3. 
4. 
5. 
6. 
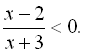
7. 
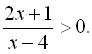
8. 
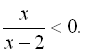
9. 
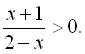
10. 
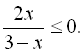
11. 
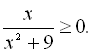
12. 
13. 
14. 
15. 
Рівень Б
1. 
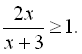
2. 
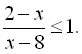
3. 
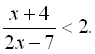
4. 
5. 
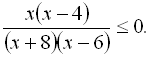
6. 
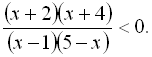
7. 
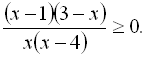
8. 
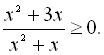
9. 
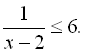
10. 
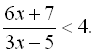
11. 
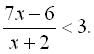
12. 
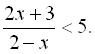
13. 
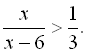
14. 
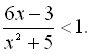
15. 
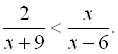
16. 
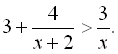
17. 
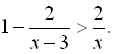
18. 
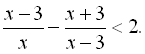
19. 
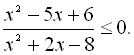
20. 
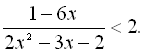
21. 
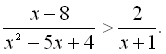
22. 
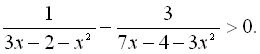
23. 
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
32. 
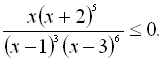
33. 
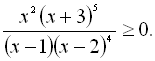
34. 
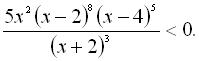
35. 
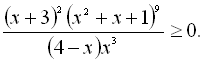
36. 
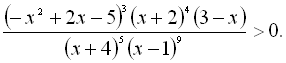
37. 
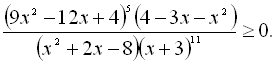
38. 
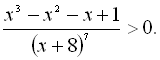
39. 
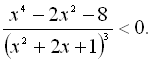
40. 
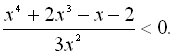
Рівень А
1. 
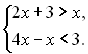
2. 
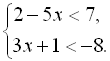
3. 
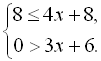
4. 
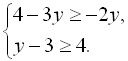
5. 
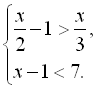
6. 
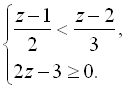
7. 
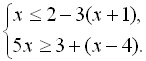
8. 
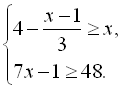
9. 
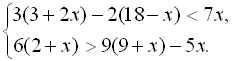
10. 
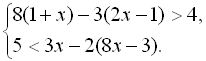
11. 
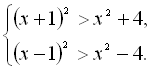
12. 
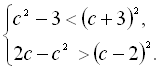
13. 
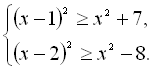
14. 
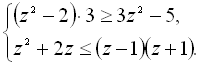
15. 
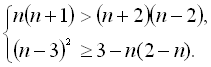
Рівень Б
1. 
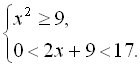
2. 
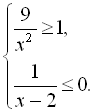
3. 
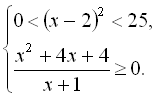
4. 
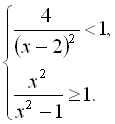
5. 
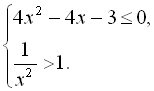
6. 
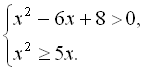
7. 
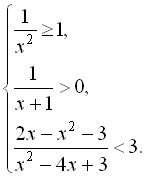
8. 
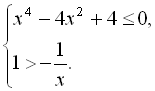
Розв’язати нерівності методом заміни змінної:
1. 
2. 
3. 
4. 
5. 
3.5. Орієнтовна контрольна робота № 3
1. Розв’язати нерівність 
.
2. Розв’язати нерівність вищого степеня
.
3. Розв’язати раціональну нерівність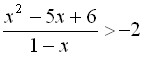 
.
4. Розв’язати систему нерівностей 
