4. ЧИСЛОВА ПОСЛІДОВНІСТЬ. ПРОГРЕСІЯ

4.1. Поняття числової послідовності

Числовою послідовністю називається функція, визначена на множині натуральних чисел. Позначається числова послідовність звичайно через , де , – n-й член послідовності.

Наведемо приклади числових послідовностей.

Приклад 1. Нехай числова послідовність задана загальним членом 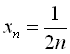. Це означає, що кожному натуральному числу n відповідає певний член послідовності . Надаючи n значення 1, 2, 3, …, дістанемо послідовність : …; … .

Приклад 2. Нехай послідовність задана формулою . Усі члени послідовності з непарними номерами дорівнюють , а з парними номерами дорівнюють 1: … . Дістаємо послідовність 1; 1; … .

Приклад 3. Для числової послідовності … формула загального члена має вигляд .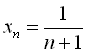

Послідовність називається зростаючою, якщо кожен її член, починаючи з другого, більший від попереднього, тобто якщо для усіх . Прикладом зростаючої послідовності можуть бути натуральні числа: 1; 2; 3; 4; …; n; … .

Послідовність називається спадною, якщо кожен її член, починаючи з другого, менший від попереднього, тобто якщо для усіх . Приклад спадної послідовності: 1; …; … .

Послідовності є скінченні і нескінченні. Скінченною є наприклад послідовність одноцифрових натуральних чисел: 1; 2; 3; 4; 5; 6; 7; 8; 9.

Із двох сусідніх членів і послідовності член називається наступним за , а – попереднім відносно .

Приклад 4. Напишіть кілька перших членів послідовності квадратів натуральних чисел. Який її n-й член?

Розв’язання

… або 4; 9; 16; 25; … . Її n-й член .

Приклад 5. Напишіть кілька перших членів послідовності натуральних чисел, кратних 3. Обчисліть її сороковий член.

Розв’язання

3; 6; 9; 12; 15; … . Перш ніж знайти сороковий член послідовності, нам потрібно знайти її n-й член. Оскільки послідовність натуральних чисел ми позначаємо , то послідовністю натуральних чисел, кратних 3, буде . Отже

4.2. Арифметична прогресія

Арифметичною прогресією називається числова послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданому до того ж самого постійного для даної послідовності числа. Позначається арифметична прогресія звичайно . називається n-м членом арифметичної прогресії.

З визначення арифметичної прогресії випливає, що . Число d називається різницею прогресії. Таким чином

.

Для того, щоб задати арифметичну прогресію , достатньо знати її перший член і різницю d. Якщо різниця арифметичної прогресії – додатне число, то така прогресія є зростаючою; якщо різниця є від’ємним числом, то спадною. Якщо різниця d арифметичної прогресії дорівнює нулю, то всі члени прогресії рівні між собою.

Характеристичні властивості арифметичної прогресії:

а) кожний член арифметичної прогресії, починаючи з другого, є середнім арифметичним сусідніх з ним членів:

, , ;

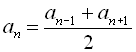б) сума членів, рівновіддалених від кінців прогресії, є величиною сталою, тобто

;

Формула п-го члена арифметичної прогресії має вигляд:

.

Формула для суми п перших членів арифметичної прогресії має вигляд

.

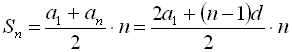     Є декілька способів задання послідовності в Maple, найприродніший seq(f(i), i=1..n). Нехай потрібно задати скінченну послідовність: 2, 4, 6, 8, 10. В цьому випадку в командний рядок вводиться:

> seq(2*i,i=1..5);

     Цю ж послідовність можна задати за допомогою оператора послідовності $:

> 2*i$i=1..5;

Сума членів скінченної числової послідовності , де , знаходиться в Maple вбудованою функцією . В загальному випадку .

Наприклад, знайти суму перших ста послідовних натуральних чисел можна таким чином:

> add(n,n=1..100);

     Суму перших двадцяти непарних натуральних чисел можна знайти так:

> add(2*n-1,n=1..20);

     У випадках, коли діапазон зміни індексу підсумовування не є числовим, а заданий символами, слід використовувати функцію , яка має потужний потенціал символьних обчислень. Виведемо за її допомогою формули суми перших п членів арифметичної прогресії, яка має вигляд …, … . Зрозуміло, що тут – перший член, – різниця арифметичної прогресії. Знаходимо дану суму:

> sum(a[1]+(k-1)*d,k=1..n);

Після спрощення отримана формула приймає знайомий вигляд:

> factor (%);

або те ж саме, .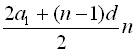

Приклад 6. Знайти одинадцятий член арифметичної прогресії , якщо її перший член дорівнює , а різниця цієї прогресії рівна 0,7.

Розв’язання

За умовою, . Для знаходження одинадцятого члена арифметичної прогресії, скористаємось формулою п-го члена арифметич-ної прогресії . Тобто 7=4.

Відповідь:

Приклад 7. Різниця арифметичної прогресії дорівнює 3, а сума перших її шести членів дорівнює 57. Знайти перший та шостий члени прогресії.

Розв’язання

За умовою . Скористаємось формулою для суми п перших членів арифметичної прогресії 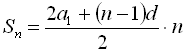. Маємо 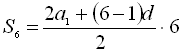, отже

.

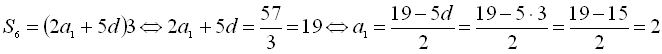Відповідь: ; .

Приклад 8. Знайти арифметичну прогресію , якщо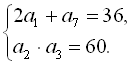

Розв’язання

Розпишемо другий, третій та сьомий члени прогресії через перший її член та різницю. Тобто Підставивши отримані дані у початкову систему, дістаємо:

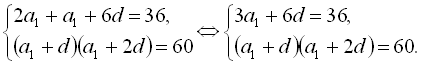
З першого рівняння системи Підставивши це значення в друге рівняння системи, дістаємо 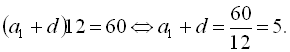Звідси маємо рівносильну початкову систему 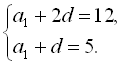Від першого рівняння системи віднімемо друге рівняння і отримаємо: . Тоді

Відповідь:

Приклад 9. Знайти суму всіх додатних парних трицифрових чисел, що діляться на 3 без остачі.

Розв’язання

Додатні парні трицифрові числа: 100, 102, 104, 106, 108, …, 994, 996, 998. З них тих, що діляться на 3: 102, 108, 114, …, 990, 996. Отримана числова послідовність є арифметичною прогресією з різницею Значить За формулою п-го члена знаходимо число членів даної прогресії 149

п=150.

Отже, шукану суму знаходимо за формулою 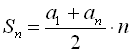. Значить .

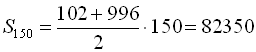Відповідь: .

Приклад 10. Знайти арифметичну прогресію, якщо сума її п перших членів .

Розв’язання

; ;

;

.

Випишемо кілька перших членів даної прогресії: -1; 3; 7; 11; … .

Відповідь: .

> restart:

eq:=sum(a[1]+(k-1)*d,k=1..n)=2*n^2-3*n;

     Спробуємо розв’язати «в лоб»

> solve(eq,{a[1],d,n});

Застосування функції isolve, що повертає цілочислові розв’язки за додаткової умови: п – натуральне число, також до успіху не приводить:

> assume(n::posint);

isolve(eq,{a[1],d,n});

Ідея розв’язання: потрібно послідовно підставити в рівняння eq два різних цілих значення . І розв’язати отриману систему двох лінійних рівнянь відносно і d. Очевидно, що найпростіше вибирати значення та :

> restart:

eq:=sum(a[1]+(k-1)*d,k=1..n)=2*n^2-3*n:

eq1:=subs(n=1,eq):eq1;

eq2:=subs(n=2,eq):eq2;

solve({eq1,eq2},{a[1],d});