4.3. Геометрична прогресія

Геометричною прогресією називається така числова послідовність , кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на те ж саме стале для даної послідовності число, відмінне від нуля. Перший член геометричної прогресії передбачається відмінним від нуля. називається п-им членом геометричної прогресії.

З визначення геометричної прогресії випливає, що 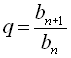. Число

називається знаменником геометричної прогресії. Таким чином,

.

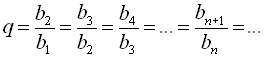Для того, щоб задати геометричну прогресію , достатньо знати її перший член і знаменник.

Якщо і , то геометрична прогресія є монотонною послідовністю. Якщо , то всі члени прогресії рівні між собою. У цьому випадку геометрична прогресія є сталою послідовністю, яка розглядається рідко.

Характеристичні властивості геометричної прогресії формулюються в такий спосіб:

а) у геометричній прогресії, усі члени якої додатні числа, будь-який її член, починаючи з другого, є середнім геометричним сусідніх з ним членів, тобто при

;

б) добуток членів, рівновіддалених від кінців геометричної прогресії, є величиною сталою, тобто

.

Формула п-го члена геометричної прогресії має вигляд

.

Формула для суми п перших членів геометричної прогресії має вигляд .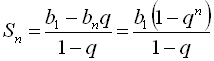

Приклад 11. Перший член геометричної прогресії дорівнює 16, а її знаменник рівний . Знайти сьомий член прогресії.

Розв’язання

За умовою, ; 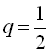. Для знаходження сьомого члена даної прогресії скористаємося формулою п-го члена геометричної прогресії . Отже, .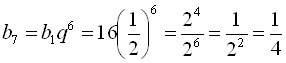

Відповідь: .

Приклад 12. Дана геометрична прогресія : -2; 8; -32; 128; … . Знайти .

Розв’язання

Знаходимо спочатку знаменник прогресії: ; .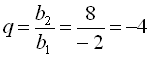

Відповідь: .

Приклад 13. У геометричній прогресії . Знайти .

Розв’язання

Знайдемо спочатку знаменник прогресій q. За умовою ; ; ;

.

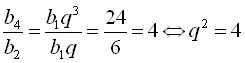Відповідь: .

Приклад 14. Знайти суму

Розв’язання

Маємо 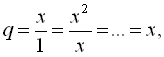. Шукану суму знаходимо за формулою суми п перших членів геометричної прогресії 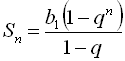, тобто .

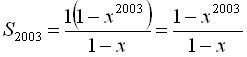Відповідь: .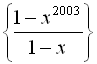

Приклад 15. У геометричній прогресії : . Знайти .

Розв’язання

Оскільки , , , то складемо таку систему рівнянь: 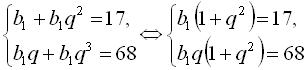. Поділивши почленно друге рівняння на перше, дістанемо 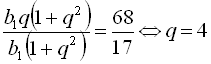. З першого рівняння системи 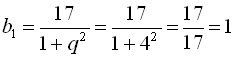. Отже, , . За формулою для суми п перших членів знаходимо .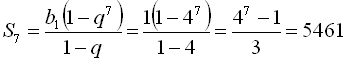

Відповідь: .

Приклад 16. Число членів геометричної прогресії парне, сума всіх членів цієї прогресії в три рази більша від суми її членів, які стоять на непарних місцях. Знайдіть знаменник прогресії.

Розв’язання

Нехай задано геометричну прогресію …, , яка має парне число членів. Сума цієї прогресії – в три рази більша від суми членів, які стоять на непарних місцях, тобто в три рази більша від . Отже, ;

.

Запишемо кожний елемент прогресії через і , тоді

. Винесемо за дужки спільні множники в обох частинах рівності:

.

Відповідь: 2.