4.4. Нескінченно спадна геометрична прогресія

Нескінченно спадною геометричною прогресією називають таку геометричну прогресію , у якої знаменник і яка містить нескінченне число доданків. Сума нескінченно спадної геометричної прогресії обчислюється за формулою .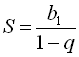

Нескінченні послідовності вводяться у вигляді seq(f(k),k=infinity), де враховано, що мовою Maple є infinity.

Нехай задана геометрична прогресія . Знайдемо суму перших п її членів:

> sum(b[1]*q^(k-1),k=1..n);

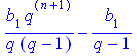
> simplify(%) assuming q<>0;

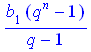
Отримана формула є формулою для обчислення суми членів геометричної прогресії.

Приклад 17. Знайти суму нескінченно спадної геометричної прогресії:

1)  … ;

2)  … .

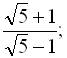
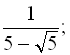
Розв’язання

1) З умови зрозуміло, що , . Тоді

.

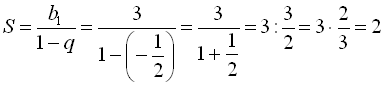2) З умови зрозуміло, що 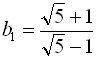, 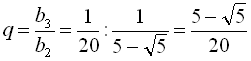. Тоді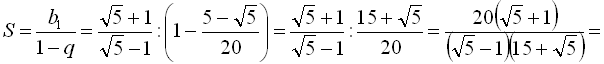

.

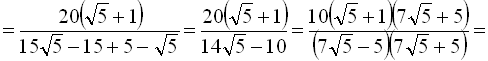
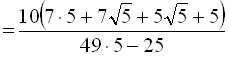
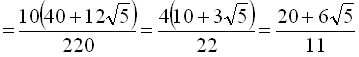Відповідь: 1) ; 2) .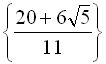

Приклад 18. Сума нескінченно спадної геометричної прогресії , а сума квадратів усіх її членів . Знайти п’ятий член прогресії.

Розв’язання

Прогресія, у якої кожним членом є квадрат , тобто

…, … має знаменник , який дорівнює квадрату знаменника заданої прогресії , тому що . Звідси маємо систему рівнянь 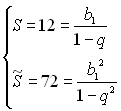. Поділивши друге рівняння системи на перше, піднесене до квадрата, дістанемо .

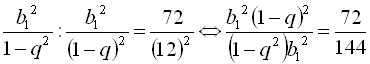З отриманої рівності, маємо .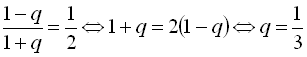

Тоді ; .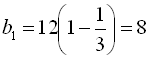

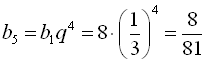Відповідь: .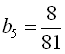

Розв’яжемо приклад 18 в Maple.

Складемо рівняння для суми нескінченно спадної геометричної прогресії та для суми квадратів усіх її членів

> restart:

eqs:=sum(b[1]*q^(k-1),k=1..infinity)=12,sum(b[1]^2*q^(2*k-2),k=1..infinity)=72:

eqs;

Знайдемо розв’язок отриманої системи

> `Розв_к`:=solve({eqs},{b[1],q}):

`Розв_к`;

Для обчислення п-го члена геометричної прогресії створимо процедуру-функцію:

> bn:=(b1,q,n)->b1*q^(n-1):

b[n]=bn(b[1],q,n);

Підставимо потрібні значення у створений вираз для обчислення п’ятого члена прогресії

> subs(`Розв_к`,n=5,%);

Очевидно, що створювати процедуру-функцію для обчислення п-го члена прогресії в даному прикладі було не обов’язково – ми могли б зразу знайти п’ятий член прогресії. Але при необхідності обчислення декількох членів прогресії такий підхід є зручним.