4.5. Комбіновані задачі на арифметичну і геометричну прогресії

Приклад 19. Чотири числа становлять арифметичну прогресію. Якщо від них відняти відповідно 10, 11, 9 і 1, то нові числа становитимуть геометричну прогресію. Знайдіть ці числа.

Розв’язання

     Нехай – члени арифметичної прогресії або де d – різниця прогресії. За умовою – члени геометричної прогресії.

     За властивістю геометричної прогресії складено систему рівнянь:

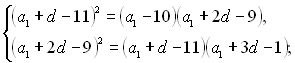
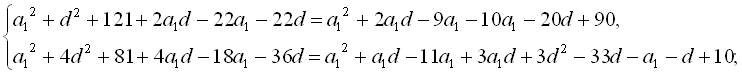
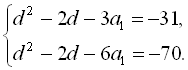Віднявши від першого рівняння останньої системи друге рівняння, отримаємо , . Тоді . Звідси або .

     Якщо і , то числа 13, 17, 21 і 25 – члени арифметичної прогресії, а числа 3, 6, 12, 24 – члени геометричної прогресії.

     Якщо і , то числа 13, 11, 9 і 7 – члени арифметичної прогресії, а числа 3, 0, 0, 6 – не є членами геометричної прогресії.

Відповідь: 13, 17, 21 і 25.

Приклад 20. Розв’язати рівняння , .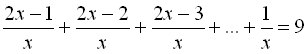

Розв’язання

     Розв’яжемо дане рівняння за допомогою системи Maple:

> isolve(sum((2*x-k)/x,k=1..2*x-1)=9,x);

4.6. Тренувальні вправи

1.  Знайти різницю і п-й член заданої арифметичної прогресії:

a) 0; 2; 4; 6; … ;

b) –1; –5; –9; –13; … ;

c) –12; –9; –6; –3; … .

2.  Записати перші п’ять членів арифметичної прогресії, якщо ; .

3.  Знайти двадцятий член арифметичної прогресії, якщо її перший член дорівнює 3, а різниця дорівнює 4.

4.  Знайти різницю арифметичної прогресії, якщо .

5.  Знайти перший член арифметичної прогресії, якщо

6.  Різниця арифметичної прогресії дорівнює 8, сума перших її п’яти членів дорівнює 115. Знайти

7.  Знайти перший член арифметичної прогресії і кількість членів п, якщо і .

8.  Знайти арифметичну прогресію, якщо: .

9.  В арифметичній прогресії : . Скільки членів прогресії треба взяти, щоб отримати суму, рівну 81?

10.  Знайти суму перших вісімнадцяти членів арифметичної прогресії , якщо .

11.  Знайти арифметичну прогресію, якщо сума її п перших членів .

12.  В арифметичній прогресії : . Знайти .

13.  В арифметичній прогресії : 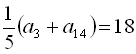. Знайти .

14.  В арифметичній прогресії : , . Знайти прогресію.

15.  – зростаюча арифметична прогресія, , . Знайти .

16.  В арифметичній прогресії : . Знайти .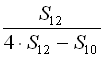

17.  Знайти арифметичну прогресію, в якій сума перших трьох членів дорівнює 24, а сума квадратів цих самих трьох членів дорівнює 290.

18.  Знайти суму всіх двоцифрових натуральних чисел.

19.  Знайти суму всіх додатних парних двоцифрових чисел, що діляться на 3 без остачі.

20.  Знайти суму всіх натуральних чисел, кратних 7 і не більших 130.

21.  Знайти суму всіх трицифрових натуральних чисел, що при діленні на 3 дають остачу 2.

22.  Знайти перший член і різницю арифметичної прогресії, якщо , .

23.  Знайти знаменник і п-ий член заданої геометричної прогресії:

a) 1; 2; 4; 8; …;

b)  …;

c)  1; -12; 144; … .

24.  Знайти знаменник геометричної прогресії, якщо , .

25.  У геометричній прогресії з додатними членами , знайти .

26.  У геометричній прогресії : , . Знайти .

27.  У геометричній прогресії : , , . Знайти і .

28.  Знайти чотири числа, що утворюють геометричну прогресію, у якій сума крайніх членів дорівнює 27, а добуток середніх дорівнює 72.

29.  У геометричній прогресії : , . Знайти .

30.  Різниця другого і першого членів геометричної прогресії дорівнює 18, різниця четвертого і третього членів дорівнює 162. Знайти прогресію.

31.  Визначити три числа, що утворюють геометричну прогресію з додатними членами, якщо їх сума дорівнює 21, а сума обернених величин дорівнює .

32.  Знайти суму нескінченно спадної геометричної прогресії:

a) 1; … ;

b) 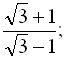 1; … .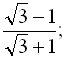

33.  Визначити суму нескінченно спадної геометричної прогресії , якщо відомо, що , .

34.  Сума членів нескінченно спадної геометричної прогресії дорівнює 18, а сума квадратів членів тієї ж прогресії дорівнює 108. Знайти і .

35.  Знайти перший член і знаменник нескінченно спадної геометричної прогресії , у якій другий член дорівнює 3, а сума членів дорівнює суми квадратів її членів.

36.  Сума нескінченно спадної геометричної прогресії , а сума квадратів усіх її членів . Знайти четвертий член прогресії.

37.  Сума трьох чисел, що утворюють арифметичну прогресію, дорівнює 21. Якщо до них додати, відповідно, числа 1, 5, 25, то вийдуть три числа, що утворюють геометричну прогресію. Знайти числа, що утворюють арифметичну прогресію.

38.  Сума трьох чисел, що є послідовними членами арифметичної прогресії, дорівнює 39. Якщо друге число зменшити на 3, а третє збільшити на 26, то вийдуть три послідовних члени геометричної прогресії. Знайдіть ці числа.

39.  Сума трьох чисел, що утворюють зростаючу геометричну прогресію, дорівнює 65. Якщо від меншого з цих чисел відняти 1, а від більшого 19, то отримані три числа утворять арифметичну прогресію. Знайти ці числа.

40.  Якщо від чотирьох чисел, що утворюють арифметичну прогресію, відняти, відповідно, 5, 10, 12 і 8, то вийдуть числа, що утворюють геометричну прогресію. Знайти числа, що утворюють арифметичну прогресію.

41.  Знайти чотири числа, перші три з яких утворюють геометричну прогресію, а останні три – арифметичну. Сума крайніх чисел дорівнює 14, а сума середніх дорівнює 12.

42.  Розв’язати рівняння:

a) 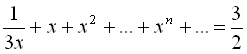, де .

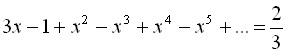b) , де .

4.7. Орієнтовна контрольна робота № 4

1. Визначити перший член і різницю арифметичної прогресії, якщо .

2. Знайти суму всіх трицифрових натуральних чисел, що діляться на 7 без остачі.

3. У геометричній прогресії : . Знайти прогресію.

4. Знайти суму нескінченно спадної геометричної прогресії:

.

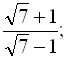
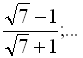5. Сума трьох перших членів зростаючої арифметичної прогресії дорівнює 15. Якщо від перших двох членів цієї прогресії відняти по одиниці, а до третього члена додати 1, то отримані три числа складуть геометричну прогресію. Знайдіть суму 10 перших членів арифметичної прогресії.