5. ТОТОЖНІ ПЕРЕТВОРЕННЯ СТЕПЕНЕВИХ ТА ІРРАЦІОНАЛЬНИХ ВИРАЗІВ. РІВНЯННЯ ТА НЕРІВНОСТІ З МОДУЛЕМ
5.1. Степінь дійсного числа з натуральним показником. Його властивості
Нехай ![]() .
. ![]() – це степінь, а – основа степеня, п – показник степеня. Степінь
– це степінь, а – основа степеня, п – показник степеня. Степінь ![]() є добутком п множників, кожний з яких дорівнює а:
є добутком п множників, кожний з яких дорівнює а: 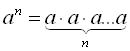 .
.
Будь-який степінь додатного числа є додатним числом, наприклад: ![]()
![]()
![]()
![]() . Парний степінь від’ємного числа є додатним числом, наприклад:
. Парний степінь від’ємного числа є додатним числом, наприклад: ![]()
![]()
![]()
![]() . Непарний степінь від’ємного числа є числом від’ємним, наприклад:
. Непарний степінь від’ємного числа є числом від’ємним, наприклад: ![]()
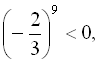
![]()
Нехай ![]()
![]()
![]()
![]() Тоді справедливі такі властивості степеня з натуральним показником:
Тоді справедливі такі властивості степеня з натуральним показником:
1) ![]() ; 2)
; 2) 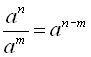 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) 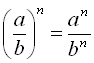 ; 6)
; 6) ![]() ; 7)
; 7) ![]() .
.
Приклад 1: Обчислити вираз 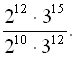
Розв’язання
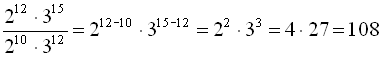 .
.
Відповідь: ![]() .
.
5.2. Степінь дійсного числа з нульовим і від’ємним цілим показником
Нехай ![]()
![]() . Припустимо за визначенням
. Припустимо за визначенням ![]()
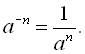
Властивості 1) – 6) степеня з натуральним показником справедливі і для степеня дійсного числа з від’ємним цілим показником. Наприклад: 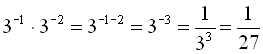 .
.
Приклад 2: Скоротити дріб 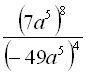 .
.
Розв’язання
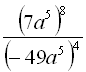
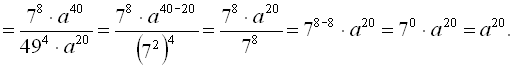
Відповідь: ![]() .
.
5.3. Властивості арифметичних коренів
Якщо ![]() і п – натуральне число, більше 1, то існує одне і тільки одне невід’ємне число х таке, що виконується рівність
і п – натуральне число, більше 1, то існує одне і тільки одне невід’ємне число х таке, що виконується рівність ![]() . Це число х називається арифметичним коренем п-го степеня з невід’ємного числа а і позначається
. Це число х називається арифметичним коренем п-го степеня з невід’ємного числа а і позначається ![]() . Число а називається підкореневим, п – показником кореня. Якщо
. Число а називається підкореневим, п – показником кореня. Якщо ![]() то звичайно пишуть
то звичайно пишуть ![]() (опускаючи показник кореня) і називають цей вираз квадратним коренем. Часто замість терміна «корінь» вживають термін «радикал».
(опускаючи показник кореня) і називають цей вираз квадратним коренем. Часто замість терміна «корінь» вживають термін «радикал».
Таким чином, згідно з визначенням запис ![]() , де
, де ![]() , означає, по-перше, що
, означає, по-перше, що ![]() і, по-друге, що
і, по-друге, що ![]() , тобто
, тобто ![]() .
.
Якщо ![]() і
і ![]() , то справедливі такі властивості:
, то справедливі такі властивості:
1) ![]() ; 2)
; 2) 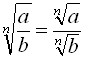 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() .
.
Корінь непарного степеня з від’ємного числа
Нехай ![]() , а п – натуральне число більше 1. Якщо п – парне число, то рівність
, а п – натуральне число більше 1. Якщо п – парне число, то рівність ![]() не виконується ні при якому дійсному значенні х. Це означає, що в області дійсних чисел не можна визначити корінь парного степеня з від’ємного числа. Якщо ж п – непарне число, то існує одне і тільки одне дійсне число х, таке, при якому
не виконується ні при якому дійсному значенні х. Це означає, що в області дійсних чисел не можна визначити корінь парного степеня з від’ємного числа. Якщо ж п – непарне число, то існує одне і тільки одне дійсне число х, таке, при якому ![]() . Це число позначають
. Це число позначають ![]() і називають коренем непарного степеня п з від’ємного числа а. Наприклад,
і називають коренем непарного степеня п з від’ємного числа а. Наприклад, ![]() , оскільки
, оскільки ![]() .
.
У випадку непарних показників коренів властивості радикалів справедливі для невід’ємних значень підкореневих виразів, справедливі і для від’ємних значень підкореневих виразів. Наприклад, ![]() для будь-яких а і b.
для будь-яких а і b.
Степінь з дробовим показником
Якщо ![]() і
і ![]() – натуральні числа,
– натуральні числа, ![]() , то
, то ![]() ; якщо
; якщо ![]() . То
. То 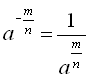 .
.
Нецілий степінь від’ємного числа не має змісту.
Степінь дійсного числа з дійсним показником має ті ж властивості, що і степінь з натуральним і цілим показником. Запишемо ці властивості, припускаючи, що ![]()


