5.4. Властивості степеня дійсного числа з дійсним показником
1) ![]() ; 2)
; 2) 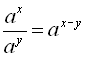 ;
;
3) ![]() ; 4)
; 4) ![]() ;
;
5) 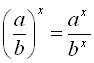 ; 6)
; 6) 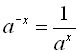 ;
;
7) ![]() ; 8)
; 8) ![]() ;
;
9) ![]() .
.
У системі Maple радикали задаються як результат піднесення до дробового степеня цілих або дробових чисел, або добування з них же квадратного кореня функцією sqrt (), або обчислення кореня п-ого степеня за допомогою функції surd (число, п). При піднесенні до степеня дробів, їх слід брати у круглі дужки, втім, як і дробовий показник степеня. Коли задають радикали, виконуються також можливі спрощення, які пов’язані з винесенням з-під знака радикала максимально можливої величини.
Наприклад,
> (9/4)^(3/2);
![]()
> sqrt(27/16);
![]()
> surd(625/81,4);
![]() .
.
Розрахунки з цілими, дробовими та ірраціональними числами є абсолютно точними, оскільки при роботі з цими типами даних програма Maple не проводить ніяких округлень на відміну від чисел з плаваючою точкою.
Приклад 3. Записати вираз у вигляді степеня 
Розв’язання
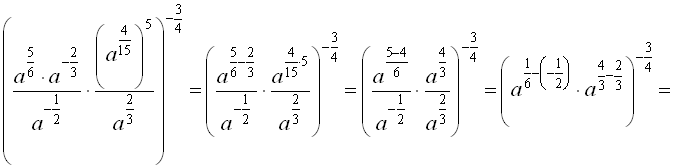
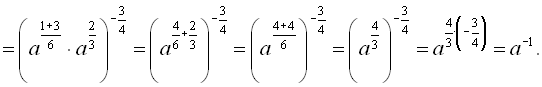
Відповідь: ![]() .
.
Приклад 4. Обчислити 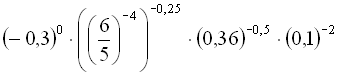 .
.
Розв’язання
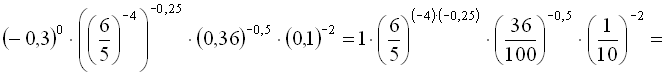
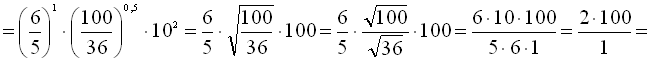
![]()
Відповідь: 200.
Здійснюючи різноманітні математичні дії (спрощення виразів, доведення теорем) часто доводиться робити ті чи інші припущення відносно деяких величин. Деякі обмеження логічно випливають з області визначення незалежних змінних, які входять у вираз, інші ми накладаємо самі. В будь-якому випадку найчастіше без введення обмежень на деякі вирази нам не обійтись. Система Maple пропонує ряд команд для введення і перевірки обмежень, накладених на деякі невідомі або, навіть, на цілі вирази. Введені обмеження використовуються командами і функціями Maple, наприклад, simplify(), sqrt(), для отримання більш простої відповіді, якщо введені обмеження дозволяють це.
Команда assume() накладає обмеження на невідомі величини Maple. Вона має такий синтаксис: assume(х, властивість). Тут х являє собою будь-яку невизначену змінну Maple або вираз з такими змінними, а параметр властивість може приймати значення, які дорівнюють назвам властивостей (спеціальним символьним іменам, які зарезервовані системою Maple для задання різноманітних обмежень на змінну чи вираз, які визначені першим параметром), імені, типу даних і числовому діапазону. Покажемо деякі найбільш уживані властивості:
Negative – від’ємні дійсні числа з інтервалу ![]()
![]() ;
;
Nonnegative – невід’ємні дійсні числа з інтервалу ![]()
![]() ;
;
Positive – додатні дійсні числа з інтервалу ![]()
![]() ;
;
Natural – натуральні числа, а також число 0;
Posint – цілі, строго більші за нуль;
Odd – непарні числа;
Even – парні числа;
Real – дійсні числа;
Rational – раціональні числа (дроби і цілі);
Irrational – ірраціональні числа;
Integer – цілі числа;
Fraction – лише дробові числа;
Prime – прості числа;
Complex – комплексні числа.
Декілька параметрів (х, властивість) можна замінити математичним відношенням, якщо, звичайно, це можливо. Наприклад, (х, negative) відповідає відношенню ![]() , (х, nonnegative) відповідає
, (х, nonnegative) відповідає ![]() і т. д.
і т. д.
Якщо на змінну накладені обмеження, то в результатах виконання дій над виразами, в які входить ця змінна, зразу ж за її іменем за замовчуванням відображається символ тильда (~).
Команда assume() може отримувати декілька пар (х, властивість) або математичних відношень як свої параметри. У цьому випадку всі задані обмеження діють одночасно. Тому накладання умов у вигляді
> assume(x>0,x<3);
відповідає тому, що змінна х може змінюватись лише у інтервалі ![]()
![]() .
.
Нове обмеження, яке накладається новою командою assume() на змінну, відміняє всі попередні обмеження. Тому послідовне задання обмежень двома командами
> assume(x>0);
> assume(x<3);
відповідає припущенню, що значення змінної х не перевищує числа 3, а не тому, що значення цієї змінної повинно належати інтервалу ![]()
![]() .
.
Якщо по ходу розв’язання задачі необхідно поступово додавати обмеження на змінну, то можна використати команду additionally(), параметри якої повністю відповідають параметрам команди assume(). В цьому випадку обмеження, які визначені командою additionally(), додаються до обмежень, які були введені командою assume() і попередніми командами additionally():
> assume(x>0);
> additionally(x<=3);
Тепер мається на увазі, що ![]() .
.
Для зняття всіх накладених раніше на змінну обмежень слід цій змінній просто присвоїти її ж символьне ім’я (ім’я змінної, яка береться в одинарні лапки). Щоб зняти всі обмеження для змінної х попередніх прикладів, слід просто виконати операцію присвоєння:
> x:=`x`;
За допомогою функції is() можна визначити, чи задовольняє деяка змінна робочого листа певній властивості. Ця функція видає значення true, якщо всі можливі значення змінної відповідають заданій властивості. Якщо хоча б одне з можливих значень не відповідає заданій властивості, то функція is() видає false. Ця функція може повернути значення FAIL, яке інформує користувача, що неможливо визначити, відповідає чи ні задана змінна заданій властивості. Це може статися або в результаті нестачі інформації відносно обмежень на змінну, або неможливості знайти логічні обмеження на змінну.
> assume(a>0);
> is(a>0);
![]()
> is(a<3);
![]()
> additionally(a<3);
> is(a<3);
![]()
Приклад 5.
a) Обчислити ![]() , якщо
, якщо ![]() ;
;
b) Відомо, що 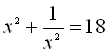 . Знайти значення виразу
. Знайти значення виразу ![]() .
.
Розв’язання
Слід зазначити, що далеко не в усіх випадках Maple може допомогти з однаковою ефективністю. Так, для прикладу 5, а) можна застосувати універсальний прийом спрощення:
> x^2-x*y+y;
![]()
> simplify(%, {x-y=-1});
![]()
Розв’язання прикладу 5, b) базується на ідеї виділення повного квадрата.
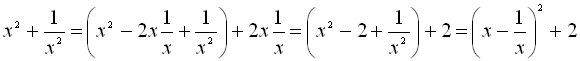 ;
;
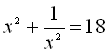
![]()
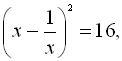
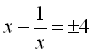 .
.
Універсальний прийом спрощення, що застосований в прикладі 5, а), тут уже не спрацьовує. Дійсно
> simplify(x-1/x, {x^2+1/x^2=18});
Error, (in simplify/siderels) side relations must be polynomials in (name or function) variables
В подібних випадках для перевірки відповіді можна застосувати команду solve
> solve(x^2+1/x^2-18);
![]() ,
,
підставити отримані корені у вираз 
> map(z->subs(x=z,x-1/x),[%]);
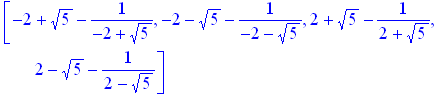
та спростити
> simplify(%);
![]()
Отримали той самий результат, що й «ручним» способом. Застосування системи в даному випадку може здатися більш складним, ніж «ручний», способом; особливо у зв’язку з необхідністю застосування команд map та subs. Але ці команди є часто вживаними, а наведений спосіб доволі універсальний. Команда map(x?f(x),L) застосовує процедуру-функцію x?f(x) до кожного операнда виразу L. В нашому прикладі операндами є корені рівняння, а процедура-функція являє собою команду підстановки subs, а саме підстановка кореня рівняння замість x у вираз  (див. С. 102).
(див. С. 102).
При перетворенні арифметичних коренів використовують їх властивості. Розглянемо декілька прикладів на застосування цих властивостей для найпростіших перетворень радикалів. При цьому будемо вважати, що всі змінні набувають тільки невід’ємного значення.
Приклад 6. Добути корінь з добутку ![]() .
.
Розв’язання
![]() .
.
Обчислимо даний приклад в Maple:
> simplify((a^4*b^8)^(1/4));
![]()
Команда simplify, яка призначена для спрощення виразу, не виконує поставлену задачу. Річ у тім, що потрібно накласти умови на підкореневий вираз:
> assume(a>0,b>0);
> simplify((a^4*b^8)^(1/4));
![]()
Приклад 7. Спростити ![]() .
.
Розв’язання
Перетворимо вираз ![]() , вносячи множник під знак кореня:
, вносячи множник під знак кореня: ![]() . Далі маємо
. Далі маємо ![]() .
.
> assume(x>0);
> simplify((x^2*x^(1/4))^(1/3));
![]()
Приклад 8. Винести множник з-під знака кореня: а) ![]() ; b)
; b)![]() .
.
Розв’язання
а) ![]() ;
;
b) ![]() .
.
Приклад 9. Спростити 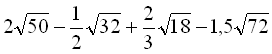 .
.
Розв’язання
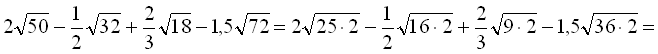
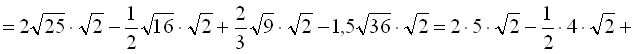
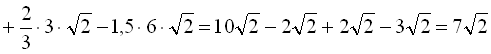 .
.
Відповідь: ![]() .
.


