5.5. Звільнення від ірраціональності в знаменнику і чисельнику дробу
Дріб можна звільнити від ірраціональності (від ірраціонального виразу) в чисельнику або в знаменнику, наприклад, так: 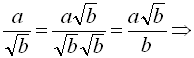 дріб
дріб ![]() звільнили від ірраціональності в знаменнику;
звільнили від ірраціональності в знаменнику; 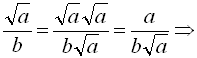 дріб
дріб ![]() звільнили від ірраціональності в чисельнику.
звільнили від ірраціональності в чисельнику.
Щоб звільнити дріб від ірраціональності в чисельнику або знаменнику, можна застосовувати формули скороченого множення, що стосовно до коренів мають вигляд:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
Вирази ![]() і
і ![]() називають взаємно спряженими виразами
називають взаємно спряженими виразами ![]()
![]() .
.
Для звільнення дробів від ірраціональності в знаменнику у системі Maple існує команда rationalize(). Вона застосовується для числових і алгебраїчних дробів. Зокрема, у випадку з алгебраїчними дробами береться до уваги лише знаменник у вигляді многочлена. Ця команда застосовується також і тоді, коли знаменник містить тригонометричні та логарифмічні функції.
Приклад 10. Звільнити дроби від ірраціональності в знаменнику:
а) 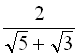 ; б)
; б) 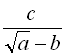 ; в)
; в)  ; г)
; г) 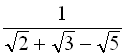 .
.
Розв’язання
а) 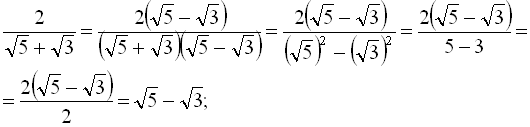
б) 
в)

г)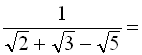

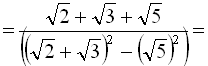
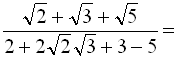

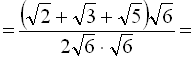

 .
.
Звільнимо дроби від ірраціональності в знаменнику у системі Maple:
> rationalize(2/(sqrt(5)+sqrt(3)));
![]()
Якщо приклад, у якому потрібно звільнитися від ірраціональності, досить довгий, або просто для зручності, команду rationalize() можна застосувати у такому вигляді:
> ex1:=1/(sqrt(2)+sqrt(3)-sqrt(5));
![]()
> rationalize(ex1);
![]()
або
> c/(sqrt(a)-b);
![]()
> rationalize(%);
![]()
Приклад 11. Обчислити значення виразу
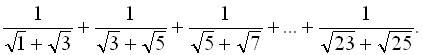
Розв’язання
Помножимо кожний доданок даної суми на вираз, спряжений до знаменника кожного із дробів:


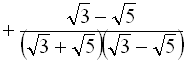

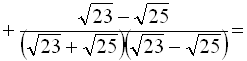
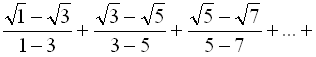

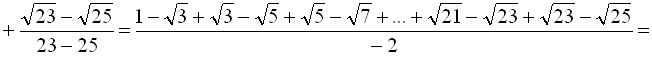
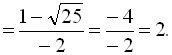
5.6. Спрощення ірраціональних виразів
Приклад 12. Спростити ![]() .
.
Розв’язання
Для того, щоб спростити даний вираз, потрібно підкореневі вирази подати у вигляді квадратів двочленів. Тобто вираз ![]() можна спочат-
можна спочат-
ку записати як ![]() або
або ![]() , відповідно вираз
, відповідно вираз ![]() записуємо як
записуємо як ![]() або
або ![]() . Тоді
. Тоді ![]()
![]() . Оскільки обидва підмодулеві вирази – додатні, то їх модулями є також додатні вирази. Отже,
. Оскільки обидва підмодулеві вирази – додатні, то їх модулями є також додатні вирази. Отже, ![]() .
.
> simplify(sqrt(11+6*sqrt(2))+sqrt(11-6*sqrt(2)));
![]()
Приклад 13. Спростити 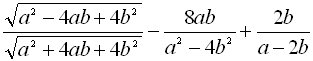 , якщо
, якщо ![]() .
.
Розв’язання

![]()
![]()
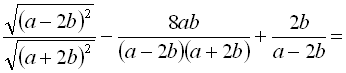
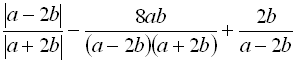 ; згідно умови задачі
; згідно умови задачі ![]() , тобто
, тобто ![]()
![]()
![]()
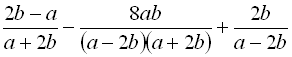
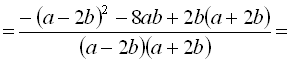

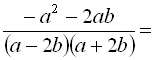
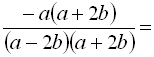
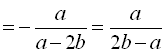 .
.
Як бачимо, у прикладі 13 накладені умови на змінні, відносно яких відбувається спрощення виразу. Якщо просто задати системі спростити вираз без накладання умов, то результат вона видасть у вигляді:
> simplify(abs(a-2*b)/abs(a+2*b)-(8*a*b)/((a*2*b)*(a+2*b))+(2*b)/(a-2*b));
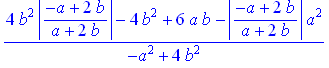
А якщо накласти перед тим умову, то отримаємо правильний результат:
> assume(a>0,(2*b)>a);
> simplify(abs(a-2*b)/abs(a+2*b)-(8*a*b)/((a-2*b)*(a+2*b))+(2*b)/(a-2*b));
![]()


