5.7. Рівняння, що містять змінну під знаком модуля

При розв’язуванні рівнянь, що містять змінну під знаком модуля, найчастіше застосовують такі методи, як:

a) розкриття модуля за визначенням;

b) метод інтервалів.

За визначенням модуля: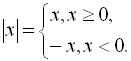

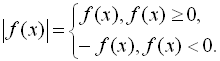
Відзначимо такі властивості модуля, які нерідко використовуються на практиці:

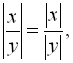
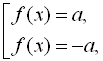Для найпростіших рівнянь з модулем слід пам’ятати, що рівняння рівносильне сукупності рівнянь якщо . Якщо ж , то рівняння розв’язків не має.

У системі Maple модуль позначається abs(). Наприклад,

> abs(x-7);

Приклад 14. Розв’язати рівняння .

Розв’язання

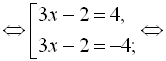
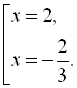
Відповідь: { 2}.

Приклад 15. Розв’язати рівняння .

Розв’язання

, оскільки з визначення модуля випливає, що для будь-якого х з області визначення функції .

Відповідь: .

Приклад 16. Розв’язати рівняння .

Розв’язання

Розглянемо два випадки, коли вираз (х+1) під знаком модуля невід’ємний і коли від’ємний. При При Звідси, початкове рівняння еквівалентне сукупності двох змішаних систем:

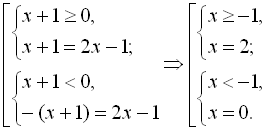Перша система має розв’язок . Друга система розв’язків не має, тому що

Відповідь:

Рівняння виду можна розв’язувати методом інтервалів, який розглянутий нижче, однак для такого рівняння швидше за все приводить до мети спосіб піднесення обох частин рівняння до квадрата, враховуючи те, що .

Приклад 17. Розв’язати рівняння .

Розв’язання

Піднесемо обидві частини рівняння до квадрата:

Відповідь: .

     Спробуємо у системі Maple спочатку задати рівняння з модулем

> abs(2*x-1)=abs(x+1);

а тепер розв’яжемо його у цій же системі:

> solve(abs(2*x-1)=abs(x+1));

5.8. Метод інтервалів (проміжків) при розв’язуванні рівнянь з модулями

Даний метод полягає в тому, що:

1) вирази, які стоять під знаком модуля, прирівнюються до нуля;

2) отримані значення відкладаються на числовій прямій, яка при цьому розбивається на інтервали (проміжки), в кожному з яких свій знак підмодулевого виразу;

3) розв’язуються отримані рівняння в кожному з інтервалів.

На практиці метод інтервалів зазвичай застосовується тоді, коли рівняння містить декілька модулів.

Розглянемо застосування методу інтервалів на прикладах.

Приклад 18. Розв’язати рівняння .

Розв’язання

1-й спосіб розв’язування:

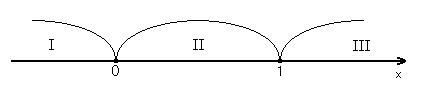
; . Наносимо на числову пряму точки і . Ці точки розбивають числову пряму на три інтервали (проміжки), у кожному з яких свій знак підмодулевого виразу. Для зручності можна позначити ці інтервали І, ІІ, ІІІ:

І: ; ІІ: ; ІІІ: .

Для інтервалу І маємо: ; .

     Звідси, дістаємо розв’язання рівняння в І інтервалі: . Однак значення не належить І інтервалу, тобто , тому в І інтервалі початкове рівняння розв'язків не має.

     Для ІІ інтервалу ; початкове рівняння має вигляд . Оскільки – це тотожність, то будь-яке є розв’язком, тобто розв’язком рівняння є весь відрізок .

     Для ІІІ інтервалу ; початкове рівняння має вигляд: . Оскільки , то в ІІІ інтервалі початкове рівняння розв’язків не має.

2-й спосіб розв’язування:

Розв’язання даного прикладу можна записати в іншій формі, застосовуючи поняття сукупності змішаних систем, тобто систем, які містять рівняння і нерівності.

     Так само, як і для 1-го способу, маємо три інтервали: І: ; ІІ: ; ІІІ: . В залежності від того, у якому інтервалі ми шукаємо розв’язок, початкове рівняння рівносильне сукупності таких змішаних систем: 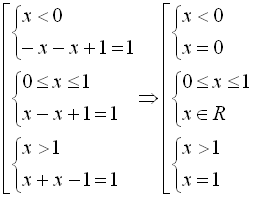. Перша і третя системи сукупності розв’язків не мають, а розв’язком другої системи є проміжок .

Відповідь: .

Приклад 19. Розв’язати рівняння .

Розв’язання

Рівняння з трьома і більше модулями зручно розв’язувати лише методом інтервалів.

; ; .

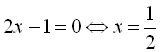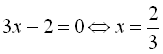Маємо чотири інтервали:

І: ;

ІІ: ;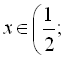

ІІІ: ;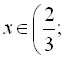

ІV: .

У І інтервалі , , . Звідси, маємо

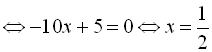. Оскільки входить в інтервал , то є розв’язком початкового рівняння.

У ІІ інтервалі ; ; .

Тоді

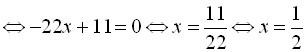. Однак .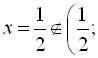

Для ІІІ інтервалу ; ; .

Звідси маємо

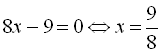. Тому що входить в інтервал , то є розв’язком початкового рівняння.

Для ІV інтервалу ; ; . Звідси дістаємо 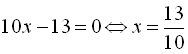. Однак значення .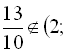

Відповідь: .

За допомогою команди eval() в системі Maple можна перевірити, чи будуть одержані значення коренями попереднього рівняння. Для цього в дужках задаємо вираз, в який ми підставляємо значення, а потім, після коми, задаємо саме значення, яке потрібно перевірити.

> eval(abs(x-2)-3*abs(2*x-1)+5*abs(3*x-2)=4,x=1/2);

> eval(abs(x-2)-3*abs(2*x-1)+5*abs(3*x-2)=4,x=9/8);

Приклад 20. Розв’язати систему рівнянь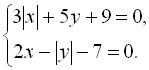

Розв’язання

В даному випадку областю допустимих значень для x і y є множина всіх дійсних чисел.

Замінимо дану систему рівнянь еквівалентною сукупністю систем: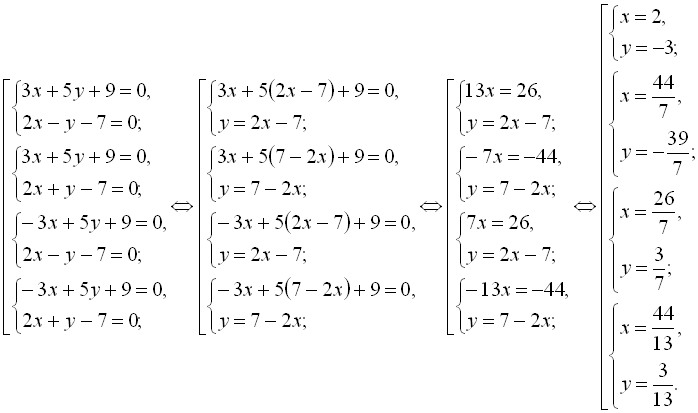

В даному прикладі робити перевірку – рутинна робота, тому доречним буде застосування команди solve для розв’язання даної системи рівнянь:

> solve({3*abs(x)+5*y+9=0,2*x-abs(y)-7=0});

Як бачимо, три пари чисел, які отримали при розв’язанні даної системи, виявились сторонніми.

Відповідь: .
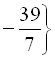