5.9. Нерівності з модулями

Перший спосіб розв’язування нерівностей з модулем. З означення модуля випливає, що для будь-якого числа а виконується нерівність . Геометрично – відстань від початку відліку (точки 0) до точки, координата якої є число а.

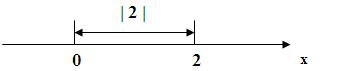
Відстань між точками а і b дорівнює . Наприклад, якщо , , то – відстань між точками з координатами 2 і 5. Або .

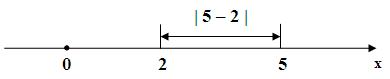
Відстань між точками 5 і –6 дорівнює: Або .

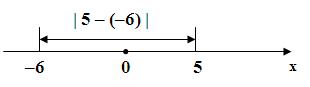
Геометрично нерівність , де , означає, що відстань від точки з координатою х до точки 0 не більша від а.

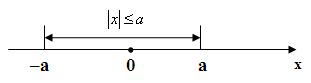
Цю властивість мають точки . Отже, нерівність означає те саме, що й подвійна нерівність . Нерівність означає те саме, що й подвійна нерівність .

Нерівність означає, що або . Нерівність означає, що або .

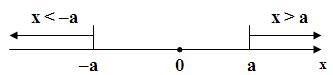
Нерівності , де , розв’язуються аналогічно, бо можуть бути зведені до попередніх заміною .

Другий спосіб розв’язування нерівностей з модулем. При розв’язуванні нерівностей, що містять змінну під знаком модуля, використовується визначення модуля функції: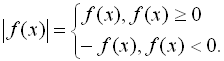

Нерівність виду , якщо ,

якщо , то нерівність розв’язків не має.

Нерівність виду 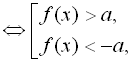якщо ;

якщо , то розв’язком нерівності буде множина припустимих значень функції ;

якщо , то розв’язком нерівності буде множина тих х, для яких .

Для розв’язання нерівностей, які містять більше одного модуля, застосовують метод інтервалів для модулів.

Приклад 21. Розв’язати нерівність

Розв’язання

Згідно з 1-им способом розв’язування нерівностей з модулем випливає, що або , тобто

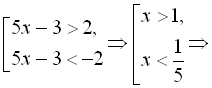
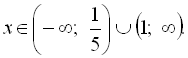
Відповідь: .

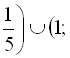
Приклад 22. Розв’язати нерівність .

Розв’язання

Оскільки , то початкова нерівність розв’язків не має.

Відповідь: .

> solve({abs(3*x+50)<-4},{x});

Як бачимо, система не видала ніяких результатів, а це, як відомо, буває у двох випадках: або розв’язок не існує, або системі не вдалося його знайти.

Приклад 23. Розв’язати нерівність .

Розв’язання

Дану нерівність можна замінити сукупністю двох систем нерівностей:

.

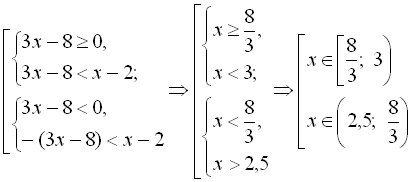
Відповідь: .

Приклад 24. Розв’язати нерівність

Розв’язання

Для розв’язування даної нерівності використаємо метод інтервалів для модулів. Відзначимо на числовій прямій точки, в яких вирази, що знаходяться під знаком модулів, перетворюються в нуль. Це точки і . Вся числова пряма розбивається цими точками на три проміжки:

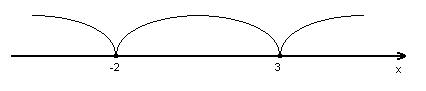
1) Розглянемо проміжок (інтервал) :

Підставивши в підмодулеві вирази замість змінної х довільне значення з даного інтервалу, виявивши тим самим знак підмодулевого виразу, отримаємо нерівність , 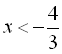. Тоді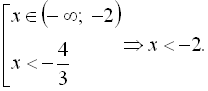

2) Розглянемо проміжок :

За тим самим принципом, що і на попередньому проміжку, маємо Тоді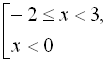

3) Розглянемо проміжок :

Маємо . Тоді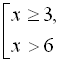

Об’єднаємо отримані розв’язки: .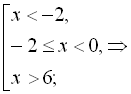

Відповідь: .

> solve({abs(x-3)+abs(x+2)-x>5},{x});

Приклад 25. Розв’язати нерівність .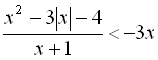

Розв’язання

Розпишемо дану нерівність у вигляді сукупності двох систем:

.

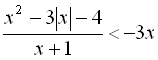
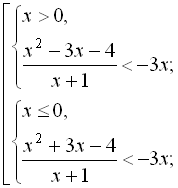
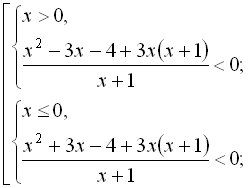
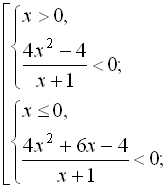
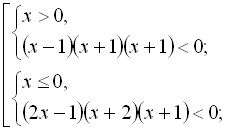
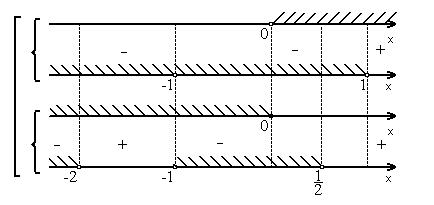
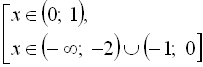
Відповідь: .