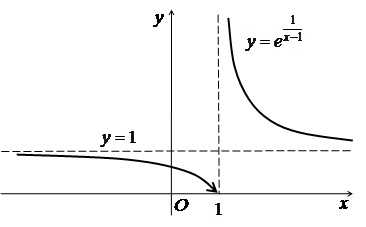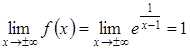2.8. Неперервність функції
Означення 2.8. Функція ![]() називається неперервною
в точці
називається неперервною
в точці ![]() (continuous function at point), якщо:
(continuous function at point), якщо:
1) вона визначена в цій точці і в деякому її околі;
2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:
![]() ,
або
,
або ![]() . (2.7)
. (2.7)
Приклад 2.30. Дослідити на неперервність функцію ![]() в точці
в точці ![]() .
.
Розв’язання.
![]()
![]()
Якщо ![]() , то
, то ![]() ;
;  - величина
обмежена, тому, за теоремою 2.4,
- величина
обмежена, тому, за теоремою 2.4, ![]() . Отже,
. Отже, ![]() , і тому, за означенням 2.8, функція
, і тому, за означенням 2.8, функція ![]() - неперервна
в точці
- неперервна
в точці ![]() .
.
Неперервність функції в точці можна означити і по-іншому.
Означення 2.9. Функція ![]() називається неперервною
в точці
називається неперервною
в точці ![]() , якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці
, якщо вона має в цій точці границю, яка
дорівнює значенню функції в точці ![]() , тобто
, тобто
![]() . (2.8)
. (2.8)
Рівність (2.8) можна деталізувати: границя зліва в
точці ![]() має дорівнювати границі справа і
дорівнювати значенню функції в цій точці:
має дорівнювати границі справа і
дорівнювати значенню функції в цій точці:
![]() . (2.8*)
. (2.8*)
Означення 2.10. Функція ![]() називається неперервною
на проміжку (continuous function on interval), якщо вона неперервна в кожній точці цього
проміжку.
називається неперервною
на проміжку (continuous function on interval), якщо вона неперервна в кожній точці цього
проміжку.
Арифметичні операції над неперервними функціями приводять знову до неперервних функцій.
Теорема 2.19. Якщо функції ![]() і
і ![]() є неперервними в точці
є неперервними в точці ![]() , тоді неперервними в цій точці будуть
також функції:
, тоді неперервними в цій точці будуть
також функції:
1) ![]() ,
, ![]() ;
;
2) ![]() ;
;
3) 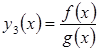 за додаткової умови
за додаткової умови ![]() .
.
Доведення. Нехай функції ![]() ,
, ![]() -неперервні в точці
-неперервні в точці ![]() .
Тоді, за означенням 2.9,
.
Тоді, за означенням 2.9, ![]() ,
, ![]() . Використаємо теореми про арифметичні
операції над функціями, що мають границю:
. Використаємо теореми про арифметичні
операції над функціями, що мають границю:
1) ![]() ;
;
2) ![]() ;
;
3) 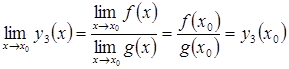 .
.
Бачимо, що означення 2.9 виконується в кожному з цих випадків. Тобто ми показали, що при виконанні арифметичних дій над неперервними функціями ми знову отримаємо неперервні функції.
Неперервність складеної функції
Теорема 2.20. Якщо функція ![]() неперервна в точці
неперервна в точці ![]() ,
а функція
,
а функція ![]() неперервна в точці
неперервна в точці ![]() , то складена функція
, то складена функція ![]() неперервна
в точці
неперервна
в точці ![]() .
.
Доведення. Справді, оскільки функція ![]() неперервна
в точці
неперервна
в точці ![]() , то
, то ![]() ;
; ![]() - неперервна
в точці
- неперервна
в точці ![]() , тому
, тому ![]() . А
це означає, що функція
. А
це означає, що функція ![]() неперервна в точці
неперервна в точці ![]() .
.
Властивості функцій, неперервних на відрізку
Теорема 2.21. (Вейєрштрасса). Якщо функція ![]() неперервна
на відрізку
неперервна
на відрізку ![]() , то вона:
, то вона:
1) обмежена (bounded function) на цьому відрізку;
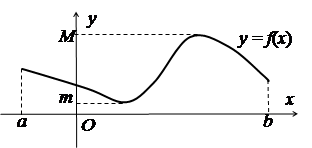 |
2) досягає на цьому відрізку свого найбільшого
![]() ,
, ![]() ;
; ![]() .
.
Рис. 2.6
Теорема 2.22. (Больцано - Коші). Якщо
функція ![]() неперервна на відрізку
неперервна на відрізку ![]() і
і ![]() , то всередині відрізка існує принаймні
одна точка с, в якій функція набуває рівного С значення (рис.
2.7).
, то всередині відрізка існує принаймні
одна точка с, в якій функція набуває рівного С значення (рис.
2.7).
![]() .
.
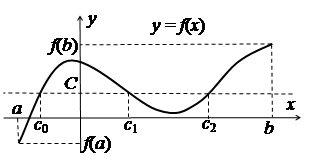
Рис. 2.7
Наслідок з теореми Больцано - Коші. Якщо функція ![]() неперервна на відрізку
неперервна на відрізку ![]() і в його кінцевих точках набуває різних
за знаком значень, то всередині відрізка існує принаймні одна точка, в якій
значення функції дорівнює нулю (рис. 2.8).
і в його кінцевих точках набуває різних
за знаком значень, то всередині відрізка існує принаймні одна точка, в якій
значення функції дорівнює нулю (рис. 2.8).
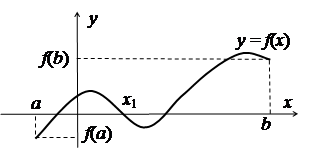
![]()
Рис. 2.8
Точки розриву функції та їх класифікація
Означення 2.11. Якщо функція ![]() в точці
в точці ![]() не є
неперервною, то точка
не є
неперервною, то точка ![]() називається точкою розриву
функції (discontinuity point).
називається точкою розриву
функції (discontinuity point).
Зауваження. Елементарна функція не може мати розривів у внутрішніх точках своєї області визначення.
Точки розриву функції можна поділити на види:
· Точки розриву першого роду (ordinary discontinuity).
Означення 2.12. Точка ![]() називається
точкою розриву функції
називається
точкою розриву функції ![]() першого роду, якщо існують скінченні односторонні границі при
першого роду, якщо існують скінченні односторонні границі при ![]() , але вони не рівні між собою.
, але вони не рівні між собою.
![]() - точка розриву першого роду
- точка розриву першого роду 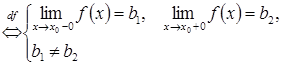 .
.
Приклад 2.31. Дослідити на розрив функцію 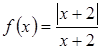 .
.
Розв’язання. Оскільки ![]() не існує, то
не існує, то ![]() -
точка розриву функції.
-
точка розриву функції.
Обчислимо односторонні границі функції в точці ![]() :
:
![]() ,
, ![]() .
.
Оскільки ![]() , то точка
, то точка ![]() є точкою розриву першого роду.
є точкою розриву першого роду.
Графік даної функції подано на рисунку 2.9.

Рис. 2.9
· Точки розриву другого роду (no ordinary discontinuity).
Означення 2.13. Точка ![]() називається точкою
розриву функції
називається точкою
розриву функції ![]() другого роду, якщо хоч би одна з односторонніх границь (зліва чи справа) при
другого роду, якщо хоч би одна з односторонніх границь (зліва чи справа) при ![]() не існує (зокрема, дорівнює
нескінченності (infinite discontinuity)).
не існує (зокрема, дорівнює
нескінченності (infinite discontinuity)).
Приклад 2.32. Дослідити на розрив функцію ![]() .
.
Розв’язання. Оскільки ![]() не існує, то
не існує, то ![]() -
точка розриву функції.
-
точка розриву функції.
Обчислимо односторонні границі функції в точці ![]() :
:
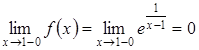 ,
(оскільки
,
(оскільки 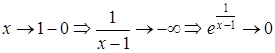 );
);
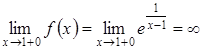 ,
(оскільки
,
(оскільки 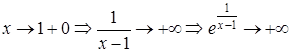 ).
).
Оскільки ![]() не існує, то точка
не існує, то точка ![]() є точкою розриву другого роду.
є точкою розриву другого роду.
Для схематичної побудови графіка функції, окрім
односторонніх границь в точці ![]() , знайдемо границю при
, знайдемо границю при
![]() :
:
|
Рис. 2.10 |
(оскільки А це означає, що пряма Графік даної функції подано на рисунку 2.10.
|
· Точки усувного розриву (removable discontinuity, removable jump).
Означення 2.14. Точка ![]() називається точкою
усувного розриву функції
називається точкою
усувного розриву функції ![]() , якщо в цій точці виконується умова
, якщо в цій точці виконується умова ![]() , але або
, але або ![]() , або
, або ![]() не існує.
не існує.
Приклад 2.33. Дослідити на розрив функцію 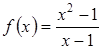 .
.
Розв’язання. Оскільки ![]() не існує, то
не існує, то ![]() -
точка розриву функції.
-
точка розриву функції.
Обчислимо границі зліва і справа в точці ![]() :
:
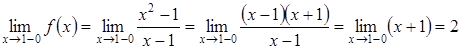 ,
,
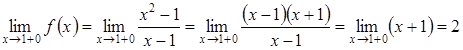 .
.
Оскільки ![]() , то точка
, то точка ![]() є точкою усувного розриву.
є точкою усувного розриву.
Отже маємо: 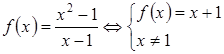 .
.
Схематичний графік зображено на рисунку 2.11.
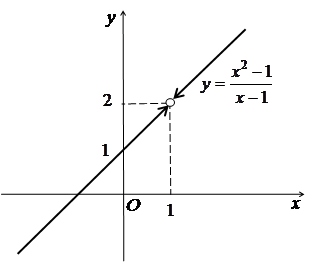
Рис. 2.11
Приклад 2.34. Дослідити функцію 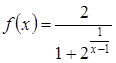 і
визначити вид точок розриву, якщо вони є. Зробити схематичний рисунок.
і
визначити вид точок розриву, якщо вони є. Зробити схематичний рисунок.
Розв’язання. Дана функція визначена для всіх ![]() . Оскільки
. Оскільки ![]() не
існує, то
не
існує, то ![]() -
точка розриву функції.
-
точка розриву функції.
Обчислимо односторонні границі в точці ![]() :
:
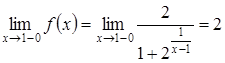 ,
(т. як
,
(т. як 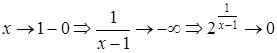 );
);
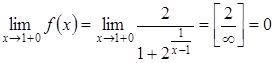 ,
(т. як
,
(т. як ![]() ).
).
Оскільки границі ![]() ,
, ![]() існують, проте
існують, проте ![]() ,
то точка
,
то точка ![]() є точкою розриву першого роду.
є точкою розриву першого роду.
В точці ![]() функція має стрибок,
що дорівнює різниці
функція має стрибок,
що дорівнює різниці
![]() .
.
Для схематичної побудови графіка функції знайдемо її
границю при ![]() :
:
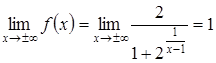 ,
(т. як
,
(т. як 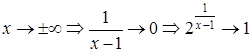 ).
).
А це означає, що пряма ![]() є горизонтальною
асимптотою.
є горизонтальною
асимптотою.
Схематичний графік даної функції зображено на рис. 2.12.
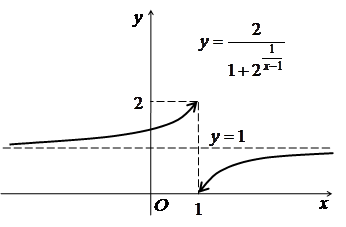
Рис. 2.12
Приклад 2.35. Дослідити задану функцію на неперервність і визначити рід точок розриву, якщо вони є. Зробити схематичний рисунок.
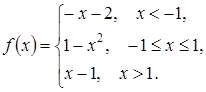
Розв’язання. Маємо неелементарну функцію, що неперервна на кожному
з інтервалів: ![]() . Очевидно, що вона може бути
розривною лише в точках
. Очевидно, що вона може бути
розривною лише в точках ![]() ,
, ![]() , в яких змінюється аналітичний вираз, що
задає функцію. Перевіримо умови неперервності в цих точках.
, в яких змінюється аналітичний вираз, що
задає функцію. Перевіримо умови неперервності в цих точках.
1) Розглянемо точку ![]() .
.
Функція визначена в цій точці і ![]() .
.
![]() ,
, ![]() .
.
Отже, існують односторонні границі функції в точці ![]() , але вони не рівні між собою. А це
означає, що дана точка є точкою розриву першого роду.
, але вони не рівні між собою. А це
означає, що дана точка є точкою розриву першого роду.
2) Розглянемо точку ![]() .
.
Функція визначена в цій точці і ![]() .
.
![]() ,
, ![]() .
.
Отже, існують односторонні границі функції в точці ![]() , вони рівні між собою і дорівнюють
значенню функції в цій точці:
, вони рівні між собою і дорівнюють
значенню функції в цій точці: ![]() . Це означає, що в
даній точці функція неперервна.
. Це означає, що в
даній точці функція неперервна.
Зробимо схематичний рисунок (рис. 2.13).
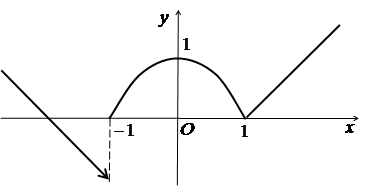
Рис. 2.13
Питання для самоперевірки
1. Яка послідовність називається збіжною? Сформулюйте означення границі послідовності.
2. Сформулюйте означення границі функції за Гейне.
3. Сформулюйте означення границі функції за Коші.
4. Сформулювати означення границі функції на нескінченності.
5. Дайте означення односторонніх границь функції в точці.
6. Сформулюйте основні теореми про границю. Будь-які чотири з них доведіть.
7. Сформулюйте і доведіть теорему про першу важливу границю.
8. Сформулюйте теорему про другу важливу границю.
9. Дайте означення нескінченно малої функції в точці. Наведіть приклад.
10.
Якщо ![]() , то що можна сказати про функцію
, то що можна сказати про функцію ![]() при
при ![]() ?
?
11. Дайте означення нескінченно великої функції в точці. Наведіть приклад.
12.
Якщо ![]() н. м. вищого порядку, ніж
н. м. вищого порядку, ніж ![]() при
при ![]() , то …
, то …
13.
Яка з наведених функцій
має вищий порядок малості при ![]() :
: ![]() ,
, ![]() ?
Відповідь обґрунтуйте.
?
Відповідь обґрунтуйте.
14. Які н. м. функції називаються функціями одного порядку? Як це записують?
15. Які н. м. функції називаються еквівалентними функціями? Як це записують?
16. Як визначається еквівалентність двох нескінченно великих функцій?
17. Сформулюйте і доведіть теореми про еквівалентні н. м. функції.
18. Перерахуйте основні еквівалентності.
19.
Яка з наведених функцій
має вищий порядок малості при ![]() :
: ![]() ,
, ![]() ?
Відповідь обґрунтуйте.
?
Відповідь обґрунтуйте.