ВСТУП ДО МАТЕМАТИЧНОГО АНАЛІЗУ

Тема 3. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ

3.1. Похідна функції

Нехай функція визначена на деякому проміжку Х і точка . Надамо аргументу функції приросту ( або ) такого, щоб точка . Функція дістане при цьому приріст

Складемо відношення

Означення 3.1. Відношення приросту функції до приросту аргументу називається середньою швидкістю зміни функції (rate of change of function).

Це відношення показує, скільки одиниць приросту функції припадає на одиницю приросту аргументу.

Означення 3.2. Границя відношення приросту функції до приросту аргументу за умови, що приріст аргументу прямує до нуля, називається швидкістю зміни функції в даній точці або її похідною (derivative) і позначається одним із символів:

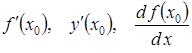Отже, за означенням

. (3.1)

Якщо похідна функції в точці існує, то функція називається диференційовною (differentiable function) в точці .

Якщо функція диференційовна в кожній точці деякого проміжку Х, то вона називається диференційовною на проміжку Х.

Операція відшукання похідної називається диференціюванням.

Приклад 3.1. Користуючись означенням похідної, знайти похідну функції .

Розв’язання. Знайдемо приріст даної функції в точці .

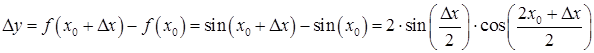звідки

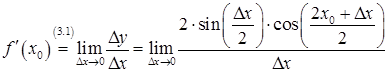оскільки ; 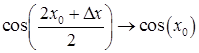при , то

Остання формула справедлива для будь-якого , тому запишемо її так:

. (3.2)

Відмітимо, що цілком аналогічно можна вивести формулу

. (3.3)

Геометричний зміст похідної (geometric sense of derivative)

Похідна функції в точці дорівнює кутовому коефіцієнту дотичної (tangent line) до графіка даної функції у точці , тобто

, (3.4)

де -кут, який утворює дотична з додатним напрямком осі

(рис. 3.1).

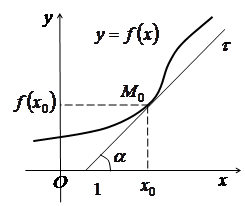
Рис. 3.1

Приклад 3.2. Користуючись означенням похідної, знайти похідну функції у точці і з’ясувати зміст одержаного результату.

Розв’язання. Знайдемо приріст даної функції в точці .

Звідки .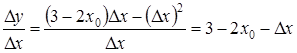

Отже .

Якщо , то . Це означає, що в даній точці функція спадає з такою ж самою швидкістю, з якою зростає аргумент.

З геометричного погляду , звідки - кут, який утворює дотична , проведена до параболи у точці (рис. 3.2).

Рис. 3.2

Зв’язок між диференційовністю функції та її неперервністю

Для існування границі (3.1) необхідно, щоб (). Тому функція повинна бути неперервною. Але не завжди існує границя (3.1) для неперервної функції. Ця умова не є достатньою а лише необхідною умовою диференційовності.

Приклад 3.3 . Чи існує ?

Розв’язання. Функція неперервна на всьому проміжку , проте в точці вона не має похідної. Дійсно:

якщо , то ;

якщо , то .

Отже, в цій точці функція не має похідної.

Теорема 3.1. Якщо функція диференційовна в точці , то вона неперервна в цій точці.

Доведення. Нехай існує . За означенням похідної . Також ми маємо , де - нескінченно мала при . Тоді , якщо . Отже, ми довели, що неперервна в точці (за означенням).