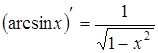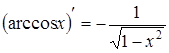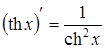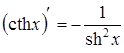3.2 Правила диференціювання (Table of Derivative Rule)

 

Теорема 3.2. Якщо функції  і  мають похідні в точці x, то справедливі формули для похідних суми, добутку та частки цих функцій:

 

1)  - (Sum Rule);

 

2)  - (Product Rule);

 

3) 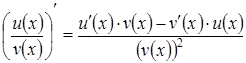, при  - (Quotient Rule).

Доведення. 1) Дійсно, розглянемо похідну суми даних функцій:

 

 

, що і потрібно було довести.

 

2) Розглянемо похідну добутку даних функцій:

 

 

 

,

що і потрібно було довести (тут використано, що , оскільки диференційовна функція  - неперервна).

 

3) Розглянемо похідну частки даних функцій за умови, що :

 

,

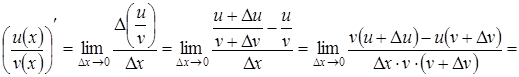
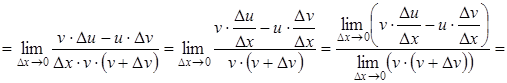
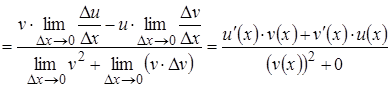що і потрібно було довести.

 

Зауваження. Сталий множник при диференціюванні виноситься за знак похідної (Constant Multiple Rule), тобто:

 

, де .

Приклад 3.4. Знайти похідну функції .

Розв’язання. За означенням функція  визначена при . Знайдемо похідну частки за теоремою 3.2, використовуючи формули (3.2), (3.3):

.

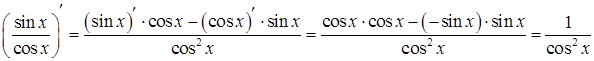Отже, при  маємо:

.                                       (3.5)

 

Похідна складеної функції (Chain Rule)

Нехай функція  визначена в деякому околі точки  і функція  визначена в деякому околі точки , таким чином визначена складена функція .

Теорема 3.3. Якщо функція  має похідну в точці  і функція  має похідну в точці , то складена функція  також має похідну в точці , причому

 

,                              (3.6)

або скорочено

                                         (3.6*)

 

Доведення. За означенням маємо:

 

.

 

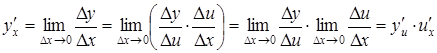Приклад 3.5. Знайти похідну функції .

Розв’язання. Приймаючи , маємо:

 

 

Тут враховано, що  також складена функція і тому за формулою (3.6) вона має похідну .

 

Похідна оберненої функції (derivative of inverse function)

Теорема 3.4. Якщо функція , ,  має обернену  і для всіх  існує похідна , то для всіх  існує похідна , причому справедлива рівність:

 

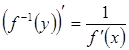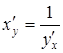 або , .                    (3.7)

 

Доведення. З означення похідної маємо:

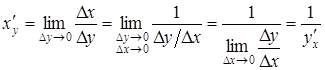, тобто , .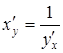

 

Приклад 3.6. Знайти похідну функції, оберненої до функції .

Розв’язання. Функція  неперервна і монотонна на проміжку 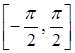. Отже, на цьому проміжку існує обернена функція, яку позначають , , 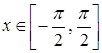. Нагадаємо, що графіки обернених функцій симетричні відносно прямої  (рис. 3.3).

 

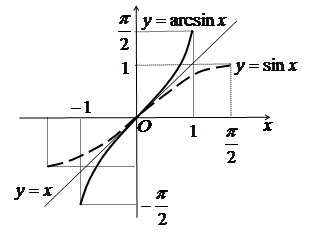
Рис. 3.3

Знаходимо похідну 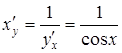. Оскільки аргументом оберненої функції є y, то виконаємо такі перетворення:

,

 

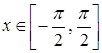
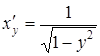знак «+» взято, оскільки при  . Отже  або

 

.

 

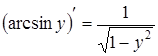Якщо аргументом є змінна х, то маємо формулу

 

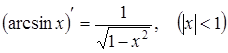.                           (3.8)

 

Продовжуючи знаходити похідні базисних елементарних функцій з урахуванням означення похідної, її властивостей та правил диференціювання можна скласти наведену нижче таблицю.

 

Таблиця похідних основних елементарних функцій

(Table of Derivative Formulas)

 

Логарифмічне диференціювання

Іноді відшукання похідної спрощується, якщо її попередньо прологарифмувати. В зв’язку з цим такий метод називається логарифмічним диференціюванням. Розглянемо як працює цей метод на прикладі.

Приклад 3.7. Знайти похідну складеної функції виду .

Розв’язання. Логарифмуючи рівність дістанемо

 

.

 

Диференціюючи обидві частини останньої рівності, матимемо:

 

,або .

 

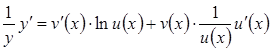Виразивши з останньої рівності  та підставивши , отримаємо

,

 

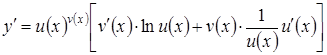цю рівність можна переписати так

 

,         (3.9)

 

де  -похідна від показникової функції,

 - похідна від степеневої функції.

Приклад 3.8. Знайти похідну .

Розв’язання. Логарифмуючи рівність дістанемо:

 

.

 

Диференціюючи обидві частини отриманої рівності за змінною х, матимемо

 

 або ,

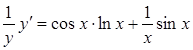звідки

.

 

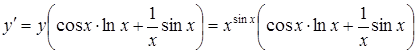Крім диференціювання степеневопоказникових функцій метод логарифмічного диференціювання доцільно застосовувати також у випадку, коли функція подана у вигляді добутку (частки) досить великої кількості функцій.

 

Приклад 3.9. Знайти похідну функції .

Розв’язання. Логарифмуючи обидві частини рівності дістанемо

 

.

 

Диференціюючи обидві частини отриманої рівності, матимемо:

 

,

або

.

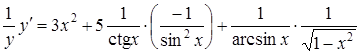Звідки

.

 

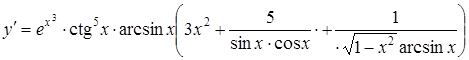Приклад 3.10. Знайти похідну функції

 

.

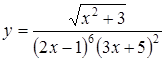Розв’язання. Логарифмуючи обидві частини рівності дістанемо

 

;

 

.

 

Диференціюючи обидві частини отриманої рівності, матимемо:

 

,

або

,

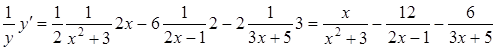звідки

.

 

 

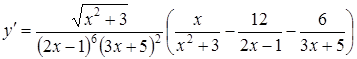Похідна функції, заданої неявно (implicit function derivative)

Якщо на деякому проміжку Х диференційовна функція  задана неявно рівнянням , то її похідну  можна знайти з рівняння

 

,

 

де  розглядається як складена функція змінної х.

 

Приклад 3.11. Знайти похідну функції, заданої неявно

 

.

 

Розв’язання. Знаходимо похідну за змінною х, пам’ятаючи, що  є функцією від х, тому

 

.

 

Розв’яжемо це рівняння відносно , отримаємо:

 

,

 

звідки

.
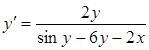