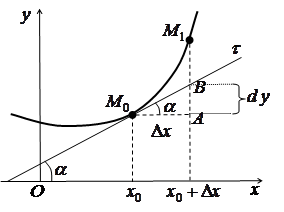3.3. Диференціал функції

 

Нехай функція  має в даній точці  скінченну похідну . Тоді , де , якщо . Звідки

 

.

 

Якщо  - нескінченно малий приріст, то доданок  є нескінченно малим вищого порядку, ніж доданок  і якщо , то  і  -нескінченно малі одного порядку.

 

Означення 3.3. Якщо функція  має похідну  в точці , то вираз  називається диференціалом (differential) функції в цій точці і позначається символом . Тобто,

 

.                                (3.10)

 

Зауваження. Диференціал функції  в даній точці є головною лінійною частиною приросту функції, пропорційною приросту аргументу з коефіцієнтом пропорційності :

 

.

 

Диференціал незалежної змінної ототожнюється з її приростом, тобто

 

.

 

Для будь-якої диференційовної в точці х функції  формулу (3.10) можна записати так:

.

Звідки отримаємо, що

,                                            (*)

 

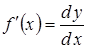тобто похідну можна розглядати як відношення двох диференціалів.

 

Правила знаходження диференціала

З правил знаходження похідної випливають правила знаходження диференціала. Якщо функції ,  -диференційовні в точці х, то

 

1) .

 

2) .

 

Зауваження. , де .

 

3) , .

 

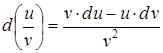Властивість інваріантності форми диференціала

Теорема 3.5. Якщо маємо складену функцію , де , причому  і  -диференційовні функції, то

 

.                                     (3.11)

 

Дійсно, , де .

Зауваження. Форма диференціала не залежить від того, є аргумент функції незалежною змінною, чи функцією цієї змінної.

 

Приклад 3.12. Знайти диференціал функції .

Розв’язання. Перший спосіб. Знаходимо похідну від заданої функції:

 

;

.

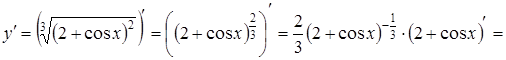
Другий спосіб. Знаходимо диференціал, використовуючи формулу (3.11):

.

 

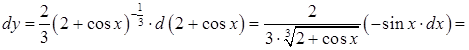
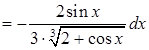Геометричний зміст диференціала (geometric sense of differential)

Нехай ,  та існує . За означенням диференціала .

Рис. 3.4

Скористаємося геометричним змістом похідної: . З трикутника  маємо:  або . Але , тому . Отже, диференціал функції  в точці  визначає приріст ординати дотичної до кривої в точці  при переході від абсциси  до абсциси       (рис. 3.4).

 

Застосування диференціала в наближених обчисленнях

З означення похідної функції в точці  випливає, що її приріст  можна подати у вигляді: , де , якщо .

Отже, при малих  має місце наближена рівність:

 

, тобто .

Звідки

.                (3.12)

 

Формула (3.12) дозволяє знаходити значення функції  в точці , якщо відомі значення  і , з точністю

 

,

де .

Приклад 3.13. Наближено обчислити значення .

Розв’язання. В даному випадку , . Покладемо , що відповідає  в градусній мірі;

.

 

За формулою (3.12), отримаємо:

 

,

 

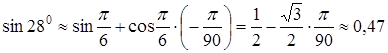тобто .

Для того, щоб оцінити абсолютну і відносну похибки, скористаємось більш точним значенням, отриманим за допомогою калькулятора: . Тоді , а відносна похибка  дорівнюватиме:

.

 

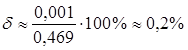Приклад 3.14. Наближено обчислити значення .

Розв’язання. В даному випадку .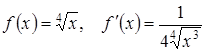

 

Нехай , , тоді  і за формулою (3.12): , отримаємо, що:

 

.

 

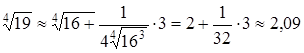Використовуючи калькулятор, отримаємо: . Тоді , а відносна похибка  дорівнюватиме:

 

.

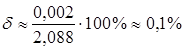Диференціювання функцій, заданих параметрично

Нехай функції  і  параметрично задають функцію , причому  і  - функції диференційовні за змінною t і .

Похідну  від функції y за змінною x знаходимо, диференціюючи  і  за змінною t (див. формулу (*)):

 

, .

Тоді

,

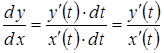тобто

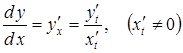.                              (3.13)

 

Приклад 3.15. Знайти похідну  функції , заданої параметрично: ,  в точці .

Розв’язання. Знаходимо похідні  та : , . За формулою (*) маємо:

 

.

 

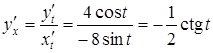Обчислимо значення параметра t в точці .

 

.

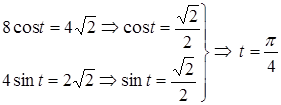Отже,  і .

 

 

Приклад 3.16. Знайти похідну  функції, заданої параметрично:

 

, .

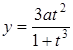Розв’язання. Знайдемо похідні  та :

 

, .

 

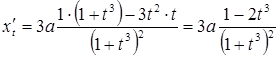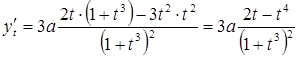Отже, 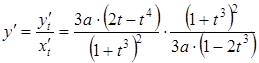, тобто .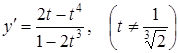