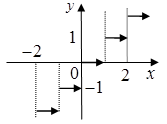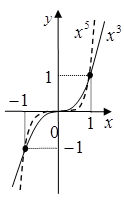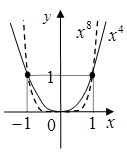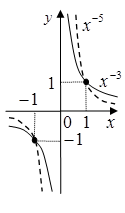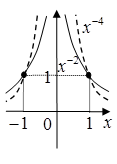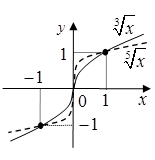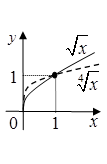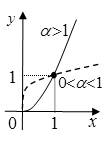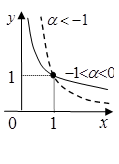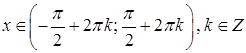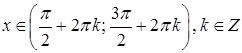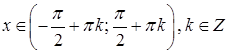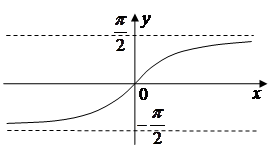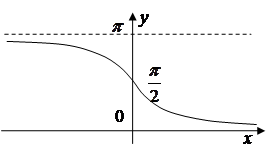1.1. Поняття функції
Нехай X та Y – дві не порожні числові множини, а x та y - відповідно їх елементи.
Означення 1.1. Якщо кожному елементу ![]() за
деяким правилом чи законом f ставиться у відповідність єдиний елемент
за
деяким правилом чи законом f ставиться у відповідність єдиний елемент ![]() , то кажуть, що на множині X задано функцію (function)
, то кажуть, що на множині X задано функцію (function) ![]() зі значеннями з
множини Y і записують
зі значеннями з
множини Y і записують
![]() .
.
При цьому x називають незалежною змінною або аргументом
(argument). Множина X
називається областю визначення функції (domain
of function) і позначається ![]() , а
множина Y називається областю значень функції (range
of function) і позначається
, а
множина Y називається областю значень функції (range
of function) і позначається ![]() .
Функціональний оператор f вказує на те, які операції треба виконати над
незалежною змінною, щоб отримати значення функції.
.
Функціональний оператор f вказує на те, які операції треба виконати над
незалежною змінною, щоб отримати значення функції.
Функцію можна задати аналітично, за допомогою таблиці та графічно.
При аналітичному способі функція задається за
допомогою формул, при побудові яких використовується запас раніше вивчених
спеціальних функцій та набір арифметичних операцій. В цьому випадку область
визначення може бути явно не вказана, але її розуміють як множину всіх значень ![]() , при яких ця формула має зміст.
, при яких ця формула має зміст.
Наприклад,
1)
функція Діріхле 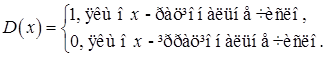 ;
;
2)
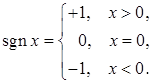
(термін «sgn» походить від латинського signum – знак);
3)
![]() , де символом
, де символом ![]() позначено цілу частину числа x.
позначено цілу частину числа x.
При табличному способі задані значення функції в окремих точках та передбачений закон, за яким змінюються значення функції між цими точками (інтерполяція). Досить часто вважають, що функція між точками змінюється лінійно (лінійна інтерполяція).
При графічному способі функція задається графіком.
Введемо на площині декартову систему координат.
Означення 1.2. Графіком функції (graph of function) ![]() називається
множина точок
називається
множина точок ![]() площини, абсциси яких
дорівнюють значенням аргументу, а ординати – відповідним значенням функції.
площини, абсциси яких
дорівнюють значенням аргументу, а ординати – відповідним значенням функції.
Побудувати графіки.
|
|
|
|
|
|
Приклад 1.1. Знайти область визначення функції ![]() .
.
Розв’язання. Функція визначена, якщо ![]() ,
тобто, якщо
,
тобто, якщо ![]() . Таким чином, областю існування функції
є відрізок
. Таким чином, областю існування функції
є відрізок ![]() , тобто
, тобто ![]() .
.
Перерахуємо основні види функцій.
Означення 1.3. Функція ![]() називається парною
(even function), якщо
називається парною
(even function), якщо ![]() для
всіх
для
всіх ![]() . Графік такої функції симетричний
відносно осі Oy.
. Графік такої функції симетричний
відносно осі Oy.
Наприклад, функції ![]() ,
, ![]() ,
, 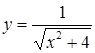 є
парними.
є
парними.
Означення 1.4. Функція ![]() називається непарною
(odd function), якщо
називається непарною
(odd function), якщо ![]() для
всіх
для
всіх ![]() . Графік такої функції симетричний
відносно початку координат.
. Графік такої функції симетричний
відносно початку координат.
Наприклад, функції ![]() ,
, ![]() ,
, ![]() є
непарними.
є
непарними.
Зауваження. Якщо функція не є парною, а також не є непарною, то вона називається функцією загального виду.
Означення 1.5. Функція ![]() називається періодичною
(periodic function), якщо існує таке додатне число T (яке
називається періодом функції), що для будь-якого значення x виконується рівність
називається періодичною
(periodic function), якщо існує таке додатне число T (яке
називається періодом функції), що для будь-якого значення x виконується рівність
![]() .
.
Наприклад, функція ![]() є
періодичною з періодом (period)
є
періодичною з періодом (period) ![]() , функція
, функція ![]() має період
має період ![]() .
.
Означення 1.6. Функція ![]() називається неспадною
(nondecreasing) [незростаючою (nonincreasing)] на проміжку X,
якщо для будь-яких
називається неспадною
(nondecreasing) [незростаючою (nonincreasing)] на проміжку X,
якщо для будь-яких ![]() виконується умова
виконується умова ![]() [
[![]() ].
].
Якщо в останніх умовах замінити знак нерівності на строгий, ми прийдемо до поняття зростаючої (increasing) [спадної (decreasing)] функції.
Функції, що зростають, спадають, не зростають, не спадають на проміжку X, називаються монотонними (monotonic) на цьому проміжку.
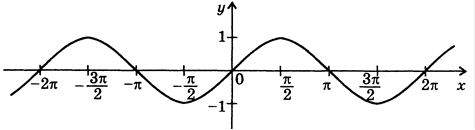
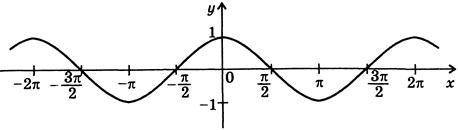
Наприклад, функція, зображена на рис.1.1, зростає на
проміжках: ![]() ,
, ![]() ;
спадає на проміжках:
;
спадає на проміжках: ![]() ,
, ![]() ,
, ![]() .
.

Рис. 1.1
Обернена функція
Якщо рівняння ![]() можна
однозначно розв’язати відносно змінної x,
тобто існує
можна
однозначно розв’язати відносно змінної x,
тобто існує ![]() таке, що
таке, що ![]() , то
функція
, то
функція ![]() або в стандартних позначеннях
або в стандартних позначеннях ![]() (позначають також
(позначають також ![]() ) називається оберненою функцією (inverse function) до
функції
) називається оберненою функцією (inverse function) до
функції ![]() .
.
Якщо областю визначення функції ![]() є множина X, а
областю значень - Y , то областю визначення оберненої функції є Y, а областю значень - X.
є множина X, а
областю значень - Y , то областю визначення оберненої функції є Y, а областю значень - X.
Графіки оберненої функції ![]() та
функції
та
функції ![]() симетричні відносно прямої
симетричні відносно прямої ![]() .
.
Можна показати, що для строго монотонної функції ![]() , визначеної на проміжку
X,
, визначеної на проміжку
X, ![]() , завжди існує строго
монотонна обернена функція
, завжди існує строго
монотонна обернена функція ![]() , визначена на
проміжку Y,
, визначена на
проміжку Y, ![]() .
.
Приклад 1.2. Знайти функцію, обернену до функції ![]() , і побудувати їх графіки.
, і побудувати їх графіки.
Розв’язання. Дана функція очевидно є строго монотонною при ![]() , тому для неї існує обернена. Розв’язуючи
рівняння відносно x, дістанемо
, тому для неї існує обернена. Розв’язуючи
рівняння відносно x, дістанемо ![]() або
в стандартних позначеннях
або
в стандартних позначеннях ![]() .
.
Отже, оберненою до заданої функції є функція ![]() .
.
Побудуємо графіки цих функцій (рис. 1.2).
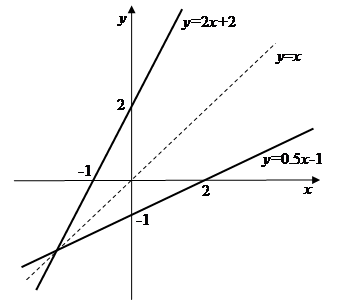
Рис. 1.2
Складена функція
Якщо аргументом функції ![]() є
функція незалежної змінної x, тобто
є
функція незалежної змінної x, тобто ![]() , то
функція
, то
функція ![]() називається складеною функцією (combined function) (суперпозицією функцій
називається складеною функцією (combined function) (суперпозицією функцій ![]() і
і ![]() ) від x. При цьому функцію f називають зовнішньою (exterior function), а функцію
) від x. При цьому функцію f називають зовнішньою (exterior function), а функцію ![]() – внутрішньою
(inner function) функцією складеної функції
– внутрішньою
(inner function) функцією складеної функції ![]() .
.
Складена функція здійснює відображення: ![]() , де
, де ![]() ,
, ![]() ,
, ![]() .
.
Наприклад, функція ![]() є
складеною степеневою функцією, аргументом якої є тригонометрична
функція, тобто
є
складеною степеневою функцією, аргументом якої є тригонометрична
функція, тобто ![]() , де
, де ![]() .
.
Складеною функцією є також степенево-показникова функція
![]() .
.
Неявна функція
Функція, задана рівнянням ![]() , що
не розв’язане відносно залежної змінної
, що
не розв’язане відносно залежної змінної ![]() ,
називається неявною функцією (implicit function) (функцією, заданою неявно).
,
називається неявною функцією (implicit function) (функцією, заданою неявно).
Наприклад, рівняння ![]() (частина
еліпса з півосями
(частина
еліпса з півосями ![]() ,
, ![]() , що
знаходиться над віссю абсцис) визначає y як
неявну функцію від x.
, що
знаходиться над віссю абсцис) визначає y як
неявну функцію від x.
Функція, задана параметрично
Кажуть, що змінна y як функція аргументу ![]() задана параметрично (parametric function), якщо обидві змінні x та y є
функціями третьої змінної t,
задана параметрично (parametric function), якщо обидві змінні x та y є
функціями третьої змінної t, ![]() :
:
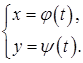
Наприклад, функцію 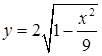 (відповідає частині еліпса з півосями
(відповідає частині еліпса з півосями ![]() ,
, ![]() , що
знаходиться над віссю абсцис) можна задати параметрично:
, що
знаходиться над віссю абсцис) можна задати параметрично:
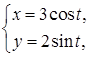 ,
, ![]() .
.
Досить часто параметричний спосіб подання функції
використовують, коли її важко (неможливо) подати у вигляді ![]() .
.
Базисні елементарні функції
До базисних елементарних функцій (basic primitive function) належать:
1) Степенева функція (Power function);
|
|
|
||
|
n непарне |
n парне |
n непарне |
n парне |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n непарне |
n парне |
|
|
|
|
|
|
|
|
|
|
|
|
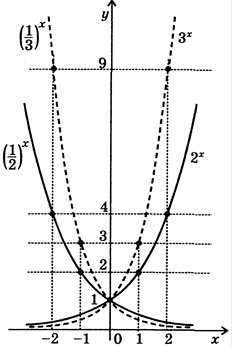
2) Показникова функція (Exponential function);
|
(при |
|
|
|
1
область визначення 2
область значень 3
зростає при 4
спадає при |
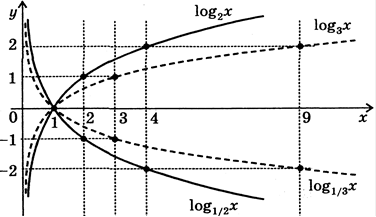
3) Логарифмічна функція (Logarithm function);
|
|
|
|
|
1
обл. визначення 2 обл. значень
3 зростає при 4 спадає при
|
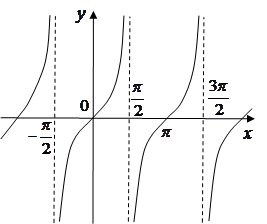
4) Тригонометричні функції (Trigonometric functions);
|
|
|
|
|
1
область визначення 2
область значень 3
період 4 функція є непарною; 5
зростає при 6
спадає при
|
|
|
|
|
|
1
область визначення 2
область значень 3
період 4 функція є парною; 5
зростає при 6
спадає при
|
|
|
|
|
|
|
1
область визначення 2
область значень 3
період 4 функція є непарною; 5
зростає при |
1
область визначення 2
область значень 3
період 4 функція є непарною; 5
спадає при |
5) Обернені тригонометричні функції (Inverse trigonometric functions).
|
|
|
|
|
|
|
|
|
1
область визначення 2
область значень 3 функція є непарною; 4 функція є зростаючою. |
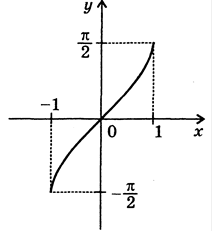
1
область визначення 2 область значень
3 функція є спадною. |
|
|
|
|
|
|
|
|
1
область визначення 2
область значень 3 функція є непарною; 4 функція є зростаючою. |
1
область визначення 2 область значень
3 функція є спадною. |
З базисних елементарних функцій за допомогою скінченної кількості арифметичних операцій та операцій суперпозиції утворюють функції, що їх називають елементарними.