1.2. Побудова графіків функцій шляхом елементарних перетворень
При побудові графіка функції 
використовують
в певній послідовності перетворення графіка функції 
. Ці
перетворення можна виконати, наприклад, в такій послідовності.
а) Будуємо графік .
б) Графік функції 
, k>0 дістанемо стискуванням графіка а) в k
разів вздовж осі абсцис до осі ординат для випадку k>1,
або розтягуванням в 1/k раз вздовж осі абсцис від осі ординат у
випадку 0<k<1. Стискування графіка вздовж осі абсцис в
k раз (k>1) здійснюється
так: абсциса кожної точки зменшується в k
раз, ордината при цьому залишається незмінною (кожна точка М(x,
y) графіка
переходить у точку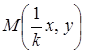 
графіка ).
Якщо ж k<0, то можна
спочатку побудувати графік 
, а потім відобразити
його симетрично відносно осі ординат.
в) Графік 
, m>0 дістанемо розтягуванням графіка б) в m
разів вздовж осі ординат відносно осі абсцис для випадку m>1, або стискуванням в 1/m
раз вздовж осі ординат відносно осі абсцис у випадку 0<m<1. Розтягування графіка вздовж осі ординат в m раз (m>1) здійснюється так: ордината кожної точки
збільшується в m раз, абсциса при цьому залишається незмінною
(кожна точка М(x,y) графіка
переходить у точку 
графіка ).
У випадку m<0 можна спочатку
побудувати графік 
, а потім відобразити його
симетрично відносно осі абсцис.
г) Графік функції 
або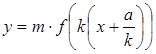 
, k>0 дістанемо паралельним перенесенням графіка в)
вліво вздовж осі Ox на 
одиниць для a>0
і вправо на 
для a<0.
д) Графік
функції дістанемо паралельним перенесенням
графіка г) вгору на b одиниць вздовж осі Oy для b>0 і вниз
на 
для b<0.
Розглянуті перетворення можна виконувати у будь-якому порядку, але величини, на які графік переноситься вздовж координатних осей, залежать від порядку перетворень.
Проілюструємо побудову графіка функції за наведеним алгоритмом.
Приклад 1.3. Побудувати графік функції 
.
Розв’язання
а) За вихідний беремо графік функції 
. Для зручності розглянемо побудову
графіка тільки на одному періоді 
.
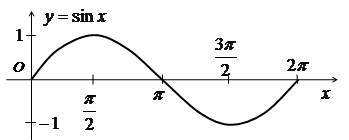
б) Оскільки
, то стискаємо графік функції в два рази вздовж осі Ox.
Дістаємо графік функції 
.
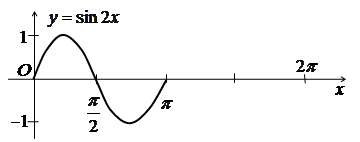
в) Розтягуємо графік функції в
три рази вздовж осі Oy, оскільки
. Дістаємо графік функції 
.
г) Симетрично відобразивши останній графік відносно осі Ox, дістанемо графік функції 
.
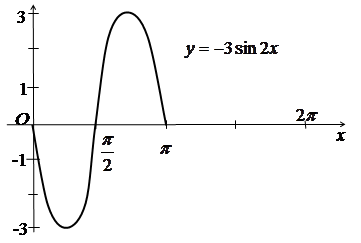
д) Отриманий графік паралельно переносимо на 
вправо вздовж осі Ox, дістанемо графік функції 
або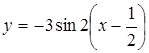 
.
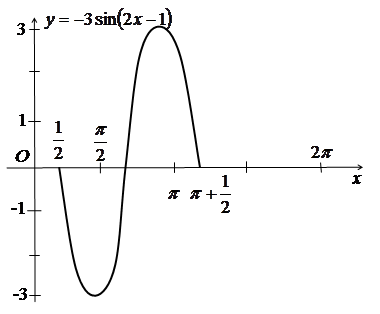
е) Нарешті, отриманий графік паралельно
перенесемо на дві одиниці вгору вздовж осі Oy,
оскільки b=2>0. Дістанемо графік функції 
(рис. 1.3).
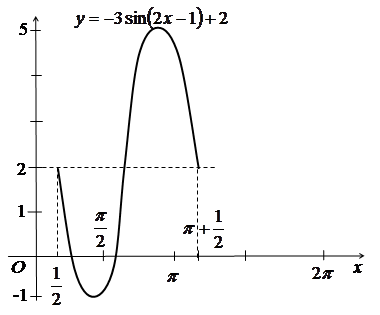
Рис. 1.3
Приклад 1.4. Побудувати графік функції 
.
Розв’язання
Область існування функції: 
.
Поділивши чисельник на знаменник, дістанемо
,
або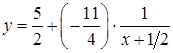 
.
Графік такої функції можна отримати з графіка функції 
за допомогою таких перетворень:
а) паралельного перенесення графіка вздовж осі абсцис на 
одиниць вліво;
б) розтягування графіка а) вздовж осі ординат в 
раз;
в) симетричного відображення графіка б) відносно осі абсцис;
в) паралельного перенесення вздовж осі ординат на 
одиниць вгору.
Будуємо схематичний графік функції (рис. 1.4).
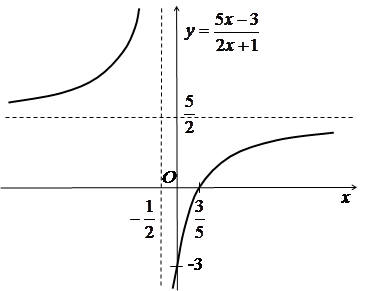
Рис. 1.4
Питання для самоперевірки
1. Сформулюйте означення функції. Вкажіть способи, якими можна задати функцію. Наведіть приклади.
2. Чи можуть точки графіка функції мати однакові абсциси? Відповідь обґрунтуйте.
3. Яку функцію називають парною? Наведіть приклади парних функцій.
4. Яку функцію називають непарною? Наведіть приклади непарних функцій.
5. Яку функцію називають складеною? Наведіть приклади складених функцій, визначте в кожному випадку зовнішню і внутрішню функції.
6. Яку функцію називають оберненою до даної? Наведіть приклади взаємно обернених функцій. Як розташовані графіки взаємно обернених функцій?
7. Яка функція називається заданою неявно? Наведіть приклади.
8. Яка функція називається параметричною? Наведіть приклади.
9. Дайте означення усіх монотонних функцій.
10. Перелічіть основні елементарні функції та вкажіть їх властивості.
11. За допомогою яких елементарних перетворень графіка
функції 
можна побудувати графік функції ?