![]() .
.
Наприклад
2·2·2=23;
7·7·7·7·7·7=76.
Розглянемо степінь
45
Число 4 називається основою степеня (основа степеня - base of power). Число 5 називається показником степеня (показник степеня - exponent).
Вираз читається так:
чотири у п'ятому степені.
Спеціальні назви степеня:
a2 читається: a в квадраті або квадрат a;
a3 читається: a в кубі або куб a.
Наприклад
23 - два в кубі;
52 - п'ять в квадраті.
Порядок дій при обчисленнях
Додавання і віднімання вважаються діями першого ступеня, мно-ження і ділення - другого ступеня, піднесення до степеня - дія третього ступеня. Обчислюючи значення виразу, спочатку виконують дії вищого ступеня, потім - нижчого. Дії одного й того самого ступеня виконуються в тому порядку, в якому вони записані. Якщо вираз містить дужки, спочатку знаходять значення виразу в дужках.
Властивості степенів
Для будь-яких x, y і додатних a і b справедливі рівності:
a·a·a·...·a=ax; a0=1; a1=a;
ax·ay=ax+y; ax:ay=ax-y;
(ax)y=axy; (ab)x=axbx;
(a/b)x=ax/bx; a-x=1/ax.
Вправи
1. Прочитати вирази:
а) a3; г) 23,237;
б) 74; д) (-2,05)2.
в) (1/2)2;
2. Піднести до степеня числа:
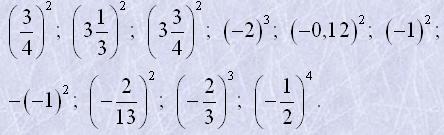
3. Розташувати числа у порядку зростання:
а) (-1,5)2; (1/7)3;
б) (+1,5)2; 0,83; (-1,1)2.
4. Розташувати числа у порядку спадання:
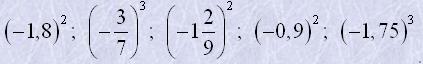
5. Записати дроби у вигляді степенів із від'ємним показником:
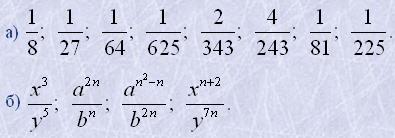
6. Виконати дії:
а) 3m·3;
б) 2n·8;
в) 7m+1·49;
г) a2m·am-1;
д) am·a3-m;
e) am+1·a1-m;
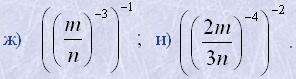
7. Знайти числові значення виразів:
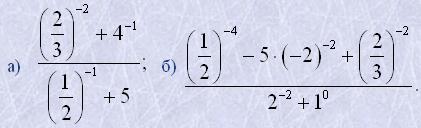

|  |
 |