Приклад 1
6, -7/12, z, x2, 3a·5b - одночлени,
Якщо одночлен містить тільки один числовий множник, до того ж поставлений на перше місце, і якщо кожна змінна входить тільки до одного множника, такий одночлен називається одночленом стандартного вигляду.
Приклад 2
3a·5c, 2x2x3, ab·8 - нестандартний вигляд;
3xy, 5a, 8 - стандартний вигляд.
Числовий множник одночлена, записаного в стандартному вигляді, називають коефіцієнтом (коефіцієнт - coefficient) цього одночлена.
Приклад 3
12xy - коефіцієнт 12.
Суму кількох одночленів називають многочленом (многочлен - polynomial).
Приклад 4
7x+2a+5 - многочлен.
Кожний доданок многочлена називається його членом.
Наприклад
многочлен 7x2+2x+7xa містить три члени: 7x2, 2x, 7a.
Многочлен, який містить два доданки, називається двочленом.
Многочлен, який містить три доданки, називається тричленом.
Подібні члени многочлену - це такі доданки, які відрізняються тільки коефіцієнтами або й зовсім не відрізняються.
Вважають, що многочлен записано в стандартному вигляді, якщо всі його члени - одночлени стандартного вигляду і серед них немає подібних.
Щоб додати два многочлени, достатньо з'єднати їх знаком плюс.
Коли пропонується знайти різницю двох многочленів, це означає - від першого з них відняти другий. Виконуючи таке завдання, після першого многочлена пишуть знак мінус і взятий у дужки другий многочлен. Розкриваючи дужки, перед якими стоїть знак мінус, знаки всіх членів, що були в цих дужках, змінюють на протилежні.
Щоб помножити многочлен на одночлен, потрібно кожний член многочлена помножити на даний одночлен і результати додати.
Приклад 5
(3x+7y)·6a=18ax+42ay.
Щоб помножити многочлен на многочлен, потрібно кожний член першого многочлена помножити на кожний член другого многочлена і отримані добутки додати.
Приклад 6
(5a+7b)·(2+4a)=5a·2+7b·2+5a·4a+7b·4a=10a+14b+20a2+28ab.
Розкласти многочлен на множники - це означає замінити його добутком кількох многочленів, тотожним даному многочлену.
Один із способів розкладання многочлена на множники - вине-сення спільного множника за дужки
ax+ay=a(x+y).
Спосіб групування
ab+ac+xb+xc=(ab+ac)+(xb+xc)=a(b+c)+x(b+c)=(b+c)(a+x).
Формули скороченого множення:
a2-b2=(a-b)(a+b);
(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3 або a3+b3+3ab(a+b);
(a-b)3=a3-3a2b+3ab2-b3 або a3-b3-3ab(a-b);
a3+b3=(a+b)(a2-ab+b2);
a3-b3=(a-b)(a2+ab+b2);
ax2+bx2+c=a(x-x1)(x-x2).
Вправи
1. Звести подібні члени:
а) 15ab+4ab-10ab; -6xy-xy+8xy;
| б) | 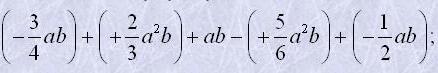 |
2. Виконати дії:
а) (x2+2xy+y2)+(2xy-x2-y2);
б) (5m2-5m+3)+(-4m2 -5m-3);
в) (10a+6b+5c-4d)+(9a-2b-4c+2d).
3. Виконати ділення:
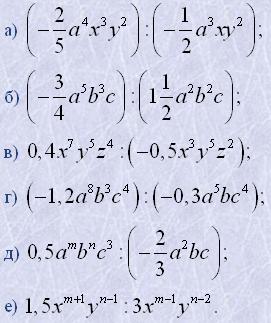
4. Спростити вираз та знайти результат:
а) bc(11c-7b)-((b-2c)·(b2-5bc)+c3), якщо b=-1/2; c=3/2;
б) (p-5n)·(3p2+2pn-7n2)-(13n(3n2-p2)-17pn2), якщо p=-3; n=-2;
в) (p-4q)·(3p2+2pq-5q2)-(12pq2-10qp2-2q2), якщо p=2; q=-3/5.
5. Виконати дії:
| а) 5(-a3b2c)3; | е) (xn+1)2; |
| б) -3(2a2b3)2; | ж) (c2n)3; |
| в) 2(-3x4y3)3; | и) (an-1)3; |
| г) -1/2(-5a3b4c2)2; | к) (-xn)2; |
| д) (ah)3; | л) (-xn)12. |
6. Подати у вигляді многочлена квадрат двочлена
| а) (0,3); | е) (xn+1)2; |
| б) -3(2a2b3)2; | ж) (c2n)3; |
| в) 2(-3x4y3)3; | и) (an-1)3; |
| г) -1/2(-5a3b4c2)2; | к) (-xn)2; |
7. Подати у вигляді квадрата двочлена:
| а) | x2+2xy+y2; | г) | a4+18a2b+81b2; |
| б) | a2+6ab+9b2; | д) | 49a2+84ab+36b2; |
| в) | 25b2+20b+4; | е) | 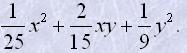 |
8. Замінити знаки "?" одночленами так, щоб рівність була правильною:
| а) (6a5+?=?+?+25x2;) | в) (?+?)=?+70b3c+49c2; |
| б) (5b2+?)2=?+?+49c4; | г) (3a3b+?)2=?+?+25b4. |
9. Подати у вигляді многочлена квадрат двочлена:
| а) | (am-bn)2; | г) | 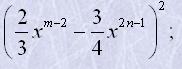 |
| б) | (2xm+3n)2; | ||
| в) | (5x2-2yn-1)2; | д) | 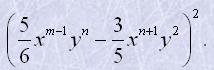 |
10. Подати вираз у вигляді квадрата двочлена:
| а) | c2+2cd+d2; |
| б) | 4a2-28ab+49b2; |
| в) | 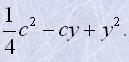 |
11. Подати вираз у вигляді суми квадратів двох виразів:
| а) 4y2-4y+1+p2; | г) x4-2x2y+5y2; |
| б) b2-6b+13; | д) a4-14a2b+53b2; |
| в) a4-6a2b2+25b4; | е) a8-10a4b2+29b4. |
12. Замінити знаки "?" одночленами так, щоб рівність була правильною:
| а) (?-?)2=81x2-?+100x4y6; | г) (?-2b)2=?-12ab+?. |
| б) (?-4x7)2=25x4y2-?+?; | |
| в) (8a3-?)2=?-?+49a8b6; |
13. Виконати дії:
| а) (3+a)·(3-a)·(3-a)·(3+a); | г) (x-y+z)·(x-y-z); |
| б) (a+2)2·(a-2)2; | д) (a-b+c)·(a+b-c); |
| в) (a+b+c)·(a+b-c); | е) (a+b+c)·(a-b-c). |
14. Скоротити дроби:
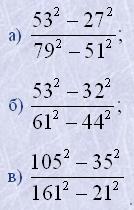
15. Подати вираз у вигляді многочлена:
| а) (x+y)3; | г) | 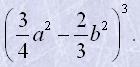 |
| б) (x2+5)3; | ||
| в) (n2+0,4m3n)3; |
16. Подати вираз у вигляді куба двочлена:
| а) m3+n2+3m2n+3mn2; | ||
| б) -b3-12b2-48b-64; | ||
| в) 27a3-13,5a2b-0,125b3; | г) | 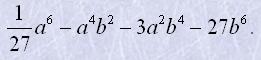 |
17. Подати у вигляді добутку:
| а) 8с3 | в) (b-c)3-b3; |
| б) (a+b)3+c3; | г) (5x+y)3-(3x-2y)3. |
18. Розкласти на множники:
| а) 13a2-52b+39; | в) a2bc+ab2c-abc2; |
| б) 12a3b-18ab2-30ab3; | г) 135a12b8+90a10b11-36a6b16. |
19. Довести тотожність:
| а) b-c-b(c-1)=c(b-1); |
| б) 2bx-a(x-b)=b(a+x)-x(a-b); |
| в) (-5a)3·(2b)4=-(10ab)3·2b; |
| г) (x-2b)(x2-5bx+b2)+(2b-x)(x2-6bx+b2)=bx(x-2b); |
| д) (a-3c)(2a2-7ac-c2)-(3c-a)(c2+7ac-a2)=a2(a-3c). |
20. Розкласти на множники:
| а) ax+ay+2x+2y; |
| б) ac+bc+a+b; |
| в) 56x2-45y-40xy+63x; |
| г) a3+a2b-a2c-abc; |
| д) 14a2c+25b2d-10abd-35abc. |
21. Довести тотожність:
| а) 5x3-2x2+5x-2=(x2+1)(5x-2); |
| б) (2ab-3c)(3ac-2b)=6a2bc-9ac2-4ab2+6bc; |
| в) 5(a+b)2-4a2-4ab=(a+b)(a+5b); |
| г) 3(x-7)2+8x-56=(x-7)(3x-13). |
22. Розкласти на множники:
| а) x2-y2; | в) 100-b4; |
| б) a2b2-c2; | г) 0,25+0,64a6. |
23. Довести тотожність:
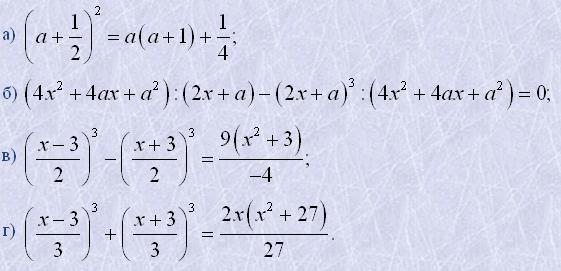
24. Розкласти на множники:
| а) (7n+8,5)2-(4n+2,5)2; |
| б) (7n+6,5)2-(2n+11,5)2; |
| в) 4b2-(x2-b2-1)2; |
| г) (2a3-4a2-a+1)2-(3a-1)2; |
| д) n4+n3-n-1; |
| е) (x+y)4-(x-y)4. |

|  |
 |