Наприклад
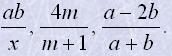
Два вирази, відповідні числові значення яких рівні при всіх допустимих значеннях змінних, називаються тотожно рівними або тотожними.
Два тотожних вирази, з'єднані знаком рівності, утворюють тотож-ність. Заміна одного виразу іншим, тотожним йому, називається тотожним перетворенням (тотожне перетворення - identical transformation) даного виразу.
Основна властивість дробу
Якщо чисельник і знаменник дробу помножити на один і той самий вираз, то дістанемо дріб, який тотожно дорівнює даному.
Наприклад
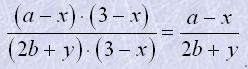
Основна властивість дробу дає можливість замінити дріб тотожно рівним йому дробом. Таке перетворення називають скороченням дробу (скорочення дробу - reduction of fraction) .
Наприклад
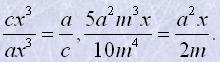
Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники, а знаменник залишити той самий. Щоб знайти різницю дробів з однаковими знаменниками, треба від чисельника зменшуваного відняти чисельник від'ємника, а знаменник залишити той самий.
Наприклад
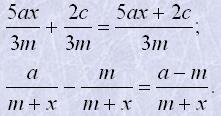
Якщо треба знайти суму або різницю дробів з різними знаменниками, то спочатку їх зводять до спільного знаменника.
Наприклад
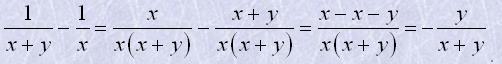
Щоб помножити дріб на дріб, треба перемножити окремо їх чисельники і окремо знаменники і перший добуток записати чисельником, а другий - знаменником дробу.
Наприклад
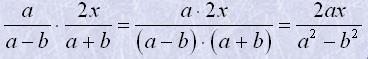
Щоб піднести дріб до степеня, треба піднести до цього степеня чисельник та знаменник і перший результат записати у чисельнику, а другий - у знаменнику дробу.
Наприклад
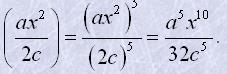
Щоб поділити один дріб на другий, треба перший дріб помножити на дріб, обернений до другого.
Наприклад
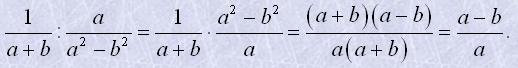
Значення дробу дорівнює нулю лише, коли чисельник перетворюється на нуль:
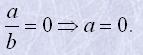
Дріб не має змісту у випадку, коли знаменник перетворюється на нуль:
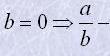
| не має змісту. |
Вираз, складений з чисел і змінних за допомогою дій додавання, віднімання, множення, ділення і піднесення до степеня, називається раціональним виразом.
Вправи
1. Поставити перед дробом знак мінус, не змінюючи величини дробу:
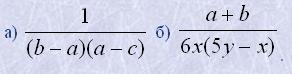
2. При яких значеннях a дріб дорівнює нулю:
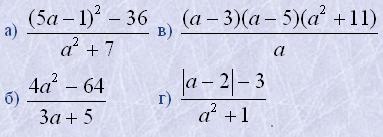
3. При яких значеннях x дріб не має змісту:

4. Скоротити дроби:
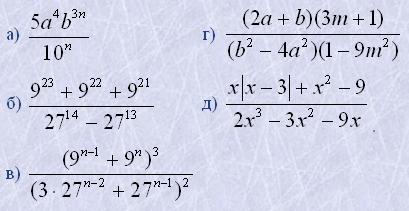
5. Привести дроби до спільного знаменника:
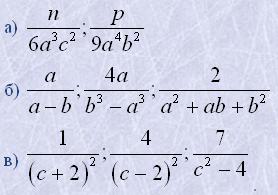
6. Виконати множення:
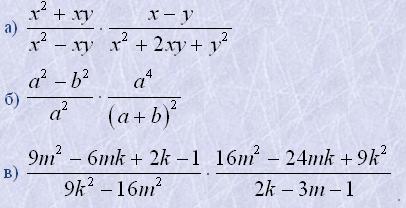
7. Виконати ділення:
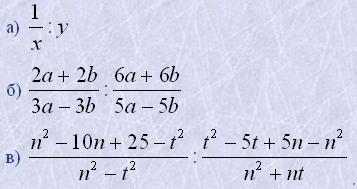
8. Виконати дії:

9. Спростити вирази:
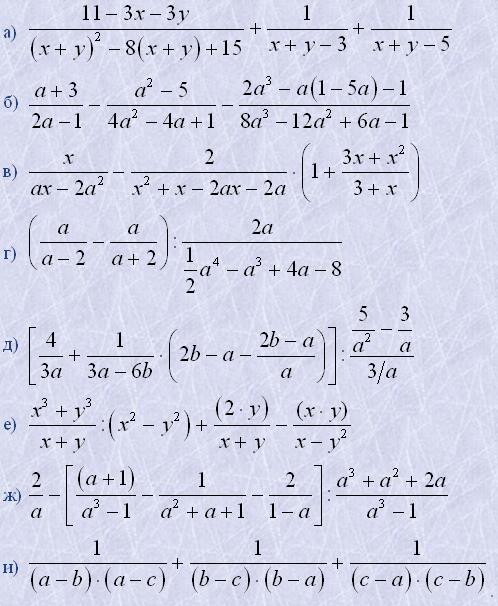

|  |
 |