Проведемо на площині дві перпендикулярні координатні прямі і , які перетинаються в початку відліку - точці (рис. 1).
Площину, на якій задано такі координатні прямі, називають координатною площиною (координатна площина - coordinate plane), пряму - віссю абсцис (вісь абсцис - abscissa axis), пряму - віссю ординат (вісь ординат - ordinate axis) , точку - початком координат (початок координат - coordinate origin).
Початок координат розбиває кожну із осей на дві півосі - додатну та від'ємну.
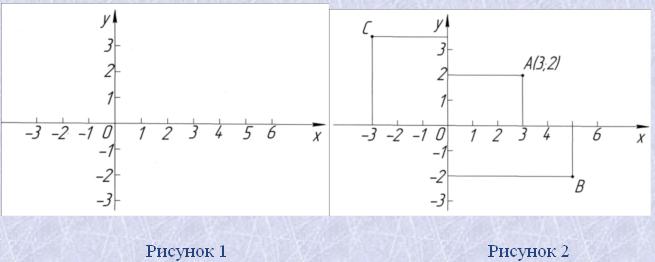
Кожній парі чисел на координатній площині відповідає єдина точка. На рис. 2 показано як позначити, наприклад, точки B(5; 2) і C( 3;3,5).
Координати точок першим використовував французький математик Рене Декарт (1596-1650). Тому їх часто називають декартовими координатами (декартові координати - Cartesian rectangular coordinates).
Якщо A(x1;y1) і B(x2;y2) - дві довільні точки і C(x;y) середина відрізка AB. Тоді
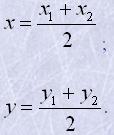
Якщо A(x1;y1) і B(x2;y2) - дві довільні точки, то відстань між точками A і B обчислюється за формулою
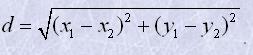
Приклад 1
Знайдіть довжину d відрізка AB та координати його середини C, якщо відомі координати точок A і B: A(1;-6), B(4;-2).
Розв'язання
Довжина відрізка AB
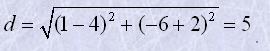
Координати точки C(x;y)
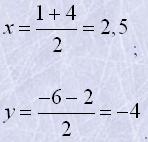
Відповідь: d=5; C(2,5;-4).
Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними x і y, яке задовольняють координати будь-якої точки фігури. І навпаки, будь-які два числа, що задовольняють це рівняння, є координатами деякої точки фігури.
Рівняння прямої в декартовій системі координат
ax+by+c=0,
де a,b,c - константи.
Рівняння кола з центром у точці A(a;b) і радіусом R
(x-a)2+(y-b)2=R2.
Приклад 2
Які з точок лежать на прямій y-x=2: (1;-1), (-1;1), (8;10); (-2;-6)?
Розв'язання
Точки, які лежать на прямі й повинні задовольняти рівняння цієї прямої.
Підставимо координати точок у рівняння прямої:
(1;-1)⇒-1-1=-2≠2 - не лежить на прямій;
(-1;1)⇒1-(-1)=2 - лежить на прямій;
(8;10)⇒10-8=2 - лежить на прямій;
(-2;6)⇒-6-(-2)=-4≠2 - не лежить на прямій;
Відповідь: (-1;1), (8;10).
Приклад 3
Знайдіть координати центра та радіус кола
x2+y2-8x+8y+7=0.
Розв'язання
Згрупуємо окремо доданки, які пропорційні x і окремо, які пропорційні y. Отримані суми доповнимо до повного квадрату:
x2+y2-8x+8y+7=(x2-8x)+(y2+8y)+7=(x2-2·4x+16-16)+(y2+2·4y+16-16)+7=
(x2-2·4x+16)+(y2+2·4y+16)-25=(x-4)2+(y+4)2-25=0.
(x-4)2+(y+4)2=52 - рівняння кола з центром у точці A(4;-4) і радіусом R=5.
Відповідь: A(4;-4), R=5.
Вправи
1. Провести осі координат, вибрати одиницю довжини на осях, побудувати точки з координатами: (1;2), (-2;1), (-1;3), (2;-1).
2. Взяти будь-які чотири точки на координатній площині. Знайти координати цих точок.
3. На прямій, паралельній осі Ox, узято дві точки. Одна з них має ординату y=2. Чому дорівнює ордината другої точки?
4. З точки A(2;3) на вісь Ox опущено перпендикуляр. Знайти координати основи перпендикуляра.
5. Знайти відстань від точки A(-3;4) до:
а) осі Ox;
б) осі Oy;
в) до початку координат.
6. На бісектрисі першої чверті взято точку з ординатою y=2. Чому дорівнює абсциса цієї точки?
7. Знайти геометричне місце точок площини Oxy, для яких x=-y.
8. Знайти координати середини відрізка з кінцями (2;0) і (0;2).
9. Дано один кінець відрізка (1;1) і його середину (2;2). Знайти другий кінець відрізка.
10. Дано три точки: A(4;-2), B(1;2), C(-2;6). Знайти відстань між цими точками, взятими попарно.
11. Знайти на осі х точку, рівновіддалену від точок (1;2) і (2;3).
12. Знайти точку, рівновіддалену від осей координат і точки (3;6).
13. Які з точок (1;2), (3;4), (-4;3), (0;5), (5;-1) лежать на колі, заданому рівнянням x2+y2=25?
14. Знайти на колі, заданому рівнянням x2+y2=169, точки:
а) з абсцисою 5;
б) з ординатою -12.
15. Дано точки A(-1;-1) і C(-4;3). Скласти рівняння кола з центром у точці C, яке проходить через точку A.
16. Знайти координати точок перетину кола x2+y2-8x-8y+7=0 з віссю Ox.
17. Скласти рівняння кола з центром у точці (1;2), яке дотикається до осі Ox.
18. Довести, що коло x2+y2+2ax+1=0 не перетинає вісь Oy.
19. Скласти рівняння геометричного місця точок, рівновіддалених від двох даних точок (0;1) і (1;2).
20. Знайти точки перетину з осями координат прямої, заданої рівнянням:
а) x+2y+3=0;
б) 3x+4y=12;
в) 3x-2y+6=0.

|  |
 |