Пряма (straight line), на якій взято початок відліку (zero point), задано одиничний відрізок (unit segment) і показано додатний напрям (positive direction) називається координатною прямою (координатна пряма - coordinate line).

Число, що показує положення точки на прямій, називається координатою (координата - coordinate) цієї точки.
Приклад 1
Точка А має координату -1,5, точка В - координату 3. Пишуть: А(-1,5), В(3).
Числа, які знаходяться праворуч (from the right of) точки 0 на координатній прямій називаються додатними (додатний - positive). Числа, які знаходяться ліворуч (from the left of) точки 0 на координатній прямій називаються від'ємними (від'ємний - negative) .
Числа, що знаходяться на одній відстані від початку координат, але лежать від нього по різні боки, називаються протилежними (протилежний - opposite) .
Наприклад, 2 і -2 - протилежні, 1,5 і -1,5 - протилежні.
Натуральні числа, протилежні їм числа і число нуль називають цілими числами (ціле число - integer).
Числа додатні (цілі і дробові), від'ємні (цілі і дробові) і нуль називаються раціональними числами (раціональне число - rational number).
Відстань (distance) від початку відліку до точки (точка - point), що зображає число, називається модулем (модуль - module) числа.
Модулем додатного числа і числа нуль є те саме число. Модулем від'ємного числа є протилежне йому число. Тобто,
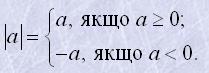
Наприклад
|2|=2; |-3|=3; |-3,5|=-3,5.
Порівняння раціональних чисел
З двох чисел меншим вважають те, яке знаходиться лівіше на коор-динатній прямій, і більшим те, яке знаходиться правіше. Будь-яке від'ємне число менше від будь-якого додатного. З двох від'ємних чисел менше те, модуль якого більший.
Приклади
-12<1, тому що -12 - від’ємне, а 1 додатне;
-12>-24, тому що |-12|<|-24|.
Додавання раціональних чисел
Сумою двох чисел з однаковими знаками є число, яке має той самий знак, що й доданки, а модуль його дорівнює сумі модулів дода-нків.
Сумою двох чисел з різними знаками є число, яке має той знак, що й доданок з більшим модулем, а модуль дорівнює різниці модулів доданків.
Приклади
8+5=13;
(-7)+12=5, тому що 12-7=5 i 12>7;
3+(-3)=0, тому що 3-3=0;
3,5+(-7,8)=-4,3, тому що 7,8-3,5=4,3 i 7,8>3,5.
Віднімання раціональних чисел
Щоб відняти будь-яке число досить до зменшуваного додати число протилежне від'ємнику:
a-b=a+(-b).
Приклади
7-15=7+(-15)=-8;
10-(-7,4)=10+7,4=17,4.
Множення раціональних чисел
Добуток двох чисел з однаковими знаками є число додатне, а модуль добутку дорівнює добутку модулів множників. Добуток двох чисел з різними знаками є число від'ємне, а модуль його дорівнює до-бутку модулів множників.
Якщо один з множників дорівнює нулю, то добуток дорівнює нулю. Навпаки: добуток може дорівнювати нулю тоді і тільки тоді, коли хоч один з множників дорівнює нулю.
Приклади
5·7=35, додатне, тому що 5 і 7 мають однакові знаки;
4,8·(-7)=-33,6, від'ємне, тому що 4,8 і -7 мають різні знаки;
23,6·0=0, тому що другий множник дорівнює 0.
Ділення раціональних чисел
Частки двох чисел з однаковими знаками є число додатне. Частка двох чисел з різними знаками є число від'ємне. Щоб знайти модуль частки, треба модуль діленого поділити на модуль дільника.
При діленні нуля на будь-яке число, що не дорівнює нулю, отримаємо нуль. Ділити на нуль не можна.
Приклади
48:6=8, додатне, тому що 48 і 6 мають однакові знаки;
44,2:(-2)=-22,1, від'ємне, тому що 44,2 і -2 мають різні знаки;
0:4,6=0,тому що дільник дорівнює 0.
Розкривання дужок
Якщо перед дужками стоїть знак плюс, то, розкриваючи дужки, знак кожного доданка, що в дужках, зберігаємо. Якщо перед дужками стоїть знак мінус, то, розкриваючи дужки, знак кожного доданка, що в дужках, змінюємо на протилежний:
a+(b+c)=a+b+c, a-(b+c)=a-b-c.
Вправи
1. Показати на координатній прямій точки, яким відповідають усі цілі числа , якщо
а) 10<|x|<18; в) 10<|x|<28;
б) |x|<10; г) |x-1|<12.
2. Розташувати у порядку зростання числа:
-15; 3; -1; -|-4|; |-2|; 0; ½; 0,9; |5|; -4.
3. Розташувати у порядку спадання числа:
-11; 0,65; |0,63|; -|5,25|; -|-5,26|; -|-2,75|; 7,4; |0|.
4. Знайти a і b, якщо |a|+|b|=0.
5. Знайти a, якщо |a|+|-a|=6.
6. Чи може сума двох від'ємних чисел бути більша їх частки?
7. Перевірити рівність: |ab|=|a|·|b| при a=-5; b=4.
8. Знайти x та y, якщо |x+y|=0.
9. Виконати дії:
а) (((-1,75)-(-3,25))·0,48+(-0,3)):0,028;
б) ((+3,28)-(-1,52)):(-24)+(-1,3)·(-0,04);
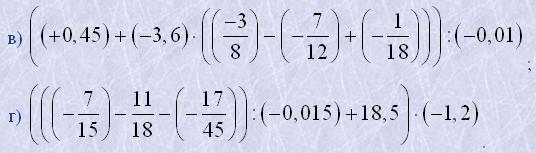
10. Від'ємник дорівнює -2,5, різниця дорівнює 14,2. Знайти зменшувальне.
11. Збільшити число 4,17 у 1,2 рази.
12. Поділити число 3,88 на число -2.

|  |
 |