Приклад 1
1:2; 13:17; 1000:1.
Основна властивість відношень
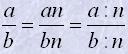
Властивості відношень 1. Відношення величин замінюють відношенням чисел, що їх вимірюють.
Приклад 2
12м:6м=12:6 або
120км:2см=12000000:2=6000000:1
2. Відношення більших чисел можна замінити відношенням менших чисел.
Приклад 3
Замість відношення 18 000:6 можна взяти відношення 3000:1.
3. Відношення дробових чисел можна замінити відношенням цілих чисел:
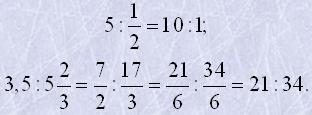
Рівність двох відношень називають пропорцією (пропорція - pro-portion).
Наприклад
2:1 = 10:5.
Числа 2 і 5 називають крайніми членами (крайній член пропорції - extreme), а числа 1 і 10 - середніми членами пропорції (середній член пропорції - mean).
Добуток крайніх членів пропорції дорівнює добутку її середніх членів.
a:b=c:d⇒a·d=b·c.
Якщо дві величини змінюються так, що відношення відповідних значень цих величин є сталим числом, то такі величини називаються прямо пропорційними (прямо пропорційний - directly proportional)
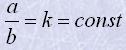 |
, k - коефіцієнт пропорційності. |
Якщо дві величини змінюються так, що добуток відповідних значень цих величин є сталим числом, то такі величини називаються обернено пропорційними (обернено пропорційний - inverse proportional)
a·b=k=const,d⇒a i b - обернено пропорційні.
Приклад 4
З 20 кг води озера Сиваш можна добути 0,5 кг солі. Скільки потрібно взяти цієї води, щоб мати 1 т солі?
Розв'язання:
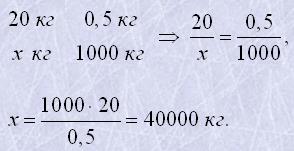
Відповідь: 40 000 кг води.
Одна сота величини або числа називається відсотком (процентом) (відсоток (процент) - per cent).
Приклад 5
Із жита отримують 80 % борошна. Скільки жита треба змолоти, щоб мати 50 кг борошна?

Відповідь: 62,5 кг жита.
Вправи
1. Скласти пропорції з рівностей:
а) 15·42=35·18;
б) 54·55=66·45;
в) 2,5·0,018=0,15·0,3.
2. Знайти невідомий член пропорції:
а) x:1=2:7; в) 45:18=180:x;
б) x:9=7:14; г) 21:x=36:12.
3. Із свіжих вишень при сушінні виходить 15% сушених вишень. Скільки сушених вишень буде з 120 кг свіжих вишень?
4. Сплав складається з міді, олова і сурми, які взято у відношенні 1:2:2. Скільки треба взяти кожної з цих речовин, щоб отримати 0,792 т сплаву?
5. Записати у відсотках:
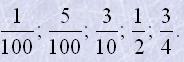
6. Скільки сухої ромашки вийде з 50 кг свіжої, якщо вона при сушінні втрачає 84 % своєї маси?
7. Знайти: а) 8 % від 1250 крб.; б) 4,5 % від 3,6 т; в) 14 % від 180 км; г) 0,5 % від 25 л.
8. Збільшити число 800 на 40 %.
9. Знайти число, якщо 8 % його дорівнює 40.
10. Свіжі гриби містять 90 % води, а сушені - 12 %. Скільки су-шених грибів вийде з 20 кг свіжих?
11. Визначити відсоток солі в розчині, якщо в 300 г розчину міс-титься 15 г солі.
12. Знайти
а) 2% від 50;
б) 6,25 % від 64;
в) 10% від 20;
г) 12,5% від 8,88.
13. Знайти число х, якщо
а) 7%x=182;
б) 60%x=23;
в) 1,6%x=4,75;
г) 7,5%x=3,3.

|  |
 |