Число 3 - ціла частина (integer part) десяткового дробу. Число 54 - дробова частина (fractional part). "," - кома (decimal point). Дріб читається так:
три цілих п'ятдесят чотири сотих.
#,# - … десятих: - дві цілих п'ять десятих;
#,## - … сотих: - сто сорок цілих двадцять три сотих;
#,### - … тисячних: - одна ціла п'ятдесят шість тисячних;
#,#### - … десятитисячних: - п'ять цілих дев'ять тисяч п'ят-десят чотири десятитисячних;
#,##### - … стотисячних: - сімсот цілих десять тисяч три стотисячних;
#,###### - … мільйонних: - три цілих вісімсот дві тисячі чотириста п'ятдесят дев'ять мільйонних.
Якщо до десяткового дробу справа приписати один або кілька нулів, то значення дробу не зміниться.
32,45,=32,450; 1,010=1,01000; 0,5=0,500.
Якщо десятковий дріб закінчується нулями, то ці нулі можна відкинути і значення дробу при цьому не зміниться.
5,000=5; 1.0030=1,003; 12,01000=12,01.
Порівняння (comparison) десяткових дробів
13,78 > 12,952, тому що 13 > 12.
Якщо ж цілі частини дробів, які порівнюють, рівні між собою, то порівнюють їхні десяткові частини: з двох десяткових дробів з однією й тією самою цілою частиною більший той, у якого кількість десятих часток більша:
13,51 > 13,48, тому що 5 > 4.
Якщо два десяткових дроби мають рівні цілі частини і десяті, то порівнюють соті і т. д. Якщо два десяткових дроби мають рівні цілі частини, рівні десяті, рівні соті, рівні тисячні і т. д. до кінця, то ці дроби рівні між собою.
13,123>13,11, тому що 2>1 ,
11,123=11,12300, тому що 11=1, 1=1, 2=2, 3=3.
Додавання десяткових дробів
Приклади
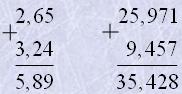
Віднімання десяткових дробів
Якщо зменшуване і від'ємник мають різну кількість знаків після коми, то можна приписати потрібну кількість нулів.
Приклади
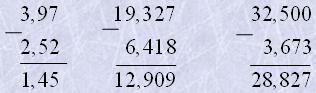
Множення десяткових дробів
2) у результаті відокремити справа комою стільки десяткових знаків, скільки їх мають обидва множники разом. Якщо в добутку, який дістанемо після множення натуральних чисел, буде менше цифр ніж їх треба, щоб відокремити комою, то зліва слід приписати потрібну кількість нулів.
Приклади
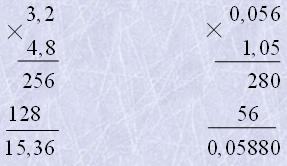
Ділення десяткових дробів на натуральне число
Якщо ціла частина діленого менша від дільника, то в частці дістанемо 0 цілих.
Якщо обчислення не закінчується діленням дробової частини діле-ного і залишається остача, то треба приписати до неї потрібну кількість нулів.
Приклади

Ділення десяткових дробів на десяткові дроби
1) помножити ділене і дільник на або 100, або 1000, або … , щоб дільник став натуральним числом;
2) ділене поділити на це натуральне число.
Приклад
3,96:16,5=(3,96·10):(16,5·10)=39,6:165=0,24.
Періодичний дріб (periodic fraction) - нескінченний десятковий дріб, у якого одна або декілька цифр повторюються в одній і тій самій послідовності. Комбінація цифр, яка повторюється, називається періодом (період - period). Період відокремлюють дужками (дужки - parenthesis).
Приклади
0,916666...=0,91(6) - період дорівнює 6;
0,2727272...0,(27)- період дорівнює 27.
Вправи
1. Прочитати дроби:
а) 1,32; в) 0,1;
б) 34,001; г) 100,0201.
2. Записати дроби під диктовку.
3. Написати звичайні дроби у вигляді десяткових:
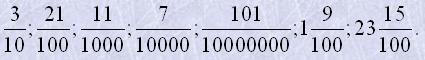
4. Скоротити дроби:
2,100; 14,7000; 0,170010; 0,930000; 181,0100; 0,150; 23,400.
5. Обчислити:
a) 5,423+3,577·(5,423-3,577);
б) (9-0,4)·(6,1-4,6)+(4,1-2,85)·(3,2-3,12);
в) (2,743-12,257)·0,01+0,047·(10000-429,5);
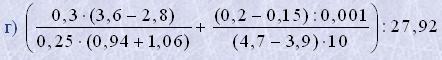
д)((0,6+0,425-0,005):0,1):(30,5-0,96:0,48+22,5).
6. Знайти x, якщо
a) 14,2-(x+3,4)=10,8;
б) 30,4x+8,176=10;
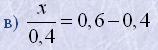
г) 3,06-0,05x+66:0,33+0,14=203
7. Подати звичайні дроби у вигляді десяткових:
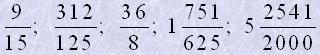
8. Подати десяткові дроби у вигляді звичайних:
0,125; 1,8; 2,24; 15,06; 0,2; 121,85.
9. Назвати період кожного дробу:
0,730303...; 9,235123423...; 0,35838383...; 269,494949... .
10. Виконати дії:
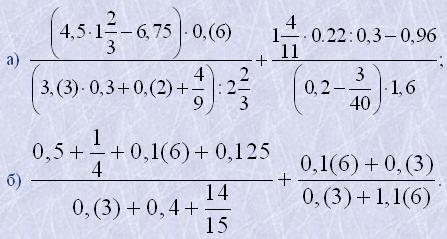
11. Зменшити число 29,4 у 2 рази.
12. Знайти добуток чисел 2,3 і 56,7.
13. Сума трьох доданків дорівнює 101,5. Перший доданок дорівнює 17,4, другий доданок у 3,31 раз більший. Знайти третій дода-нок.
14. Купили стіл і 6 стільців, заплатили всього 87,8 грн. Скільки коштував один стілець, якщо стіл коштував 38 грн?
15. Синові на штани потрібно 0,7 м тканини, а батькові в 1,8 раз більше. На скільки метрів тканини батькові треба більше?

|  |
 |