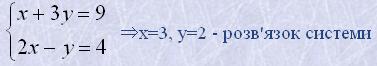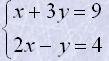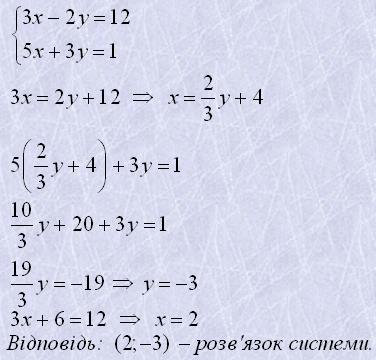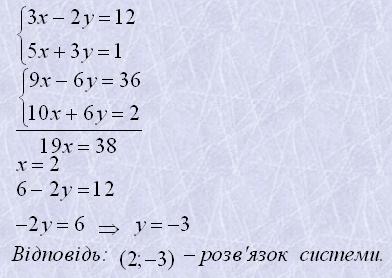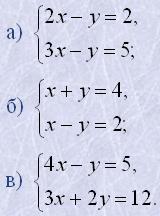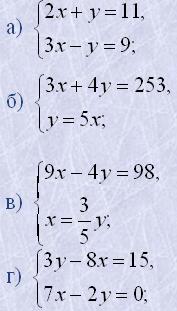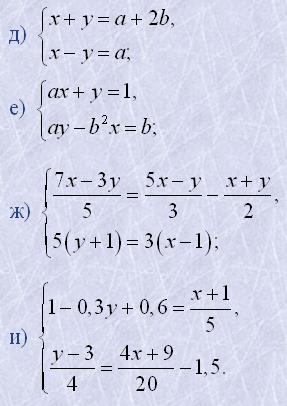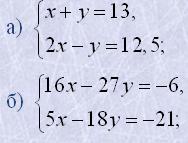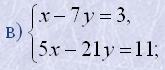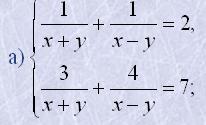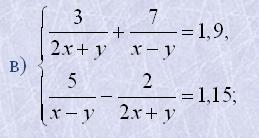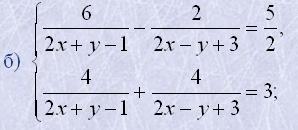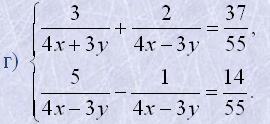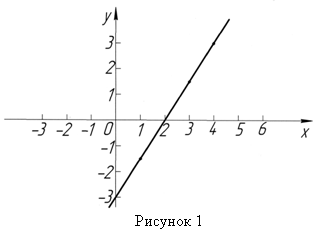
Цю пряму називають графіком (графік - graph) даного рівняння. Графік кожного рівняння першого степеня з двома змінними - пряма.
Якщо потребується знайти спільні розв'язки двох чи кількох рівнянь, то говорять, що ці рівняння утворюють систему.
Розв'язком системи рівнянь називають спільний розв'язок усіх її рівнянь.
Наприклад
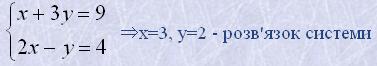
Розв'язувати системи рівнянь можна графічним способом.
Розв'яжемо, наприклад, систему
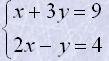
Для цього побудуємо на одній координатній площині графіки обох її рівнянь (рис. 2).
Побудовані графіки перетинаються в точці А(3; 2). Тому пара чисел (3; 2) - єдиний розв'язок даної системи рівнянь.
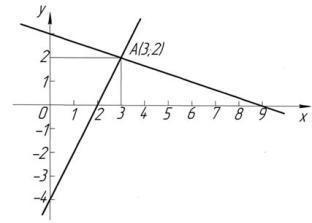
Рисунок 2
Щоб розв'язати систему рівнянь способом підстановки (метод під-становки - substitution method), треба:
а) виразити з якого-небудь її рівняння одну змінну через другу;
б) підставити в інше рівняння системи замість цієї змінної здобутий вираз;
в) розв'язати утворене рівняння з однією змінною;
г) знайти відповідне значення другої змінної.
Приклад 1
r>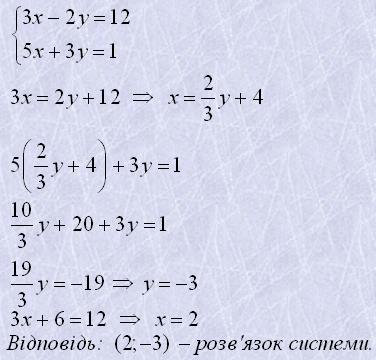
Щоб розв'язати систему методом додавання потрібно:
а) зробити коефіцієнти при одній змінній у першому і другому рів-няннях протилежними;
б) почленно додати ліві і праві частини рівнянь;
в) розв'язати утворене рівняння з однією змінною;
г) знайти відповідне значення другої змінної.
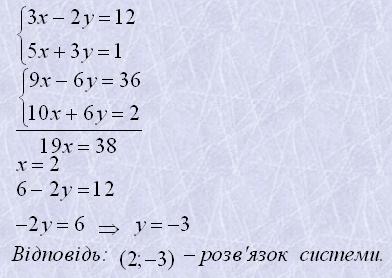
Вправи
>1. Розв'язати графічним методом системи рівнянь:
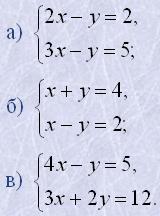
2. Розв'язати методом підстановки системи рівнянь:
3. Розв'язати методом додавання системи рівнянь:
4. Розв'язати системи введенням додаткових невідомих:
5. На будівництві працювало 50 мулярів і теслярів. Згодом кількість мулярів збільшилась у 2 рази, а теслярів у 3 рази і всіх стало 130. Скільки спочатку було мулярів і теслярів на будівництві?
6. Швидкість моторного човна за течією 23 км/год, а проти течії - 17 км/год. Знайти власну швидкість човна і швидкість течії.
7. Знайти два числа, якщо половина їх суми дорівнює 71, а половина різниці 31.
8. 20% першого числа на 15 менші, ніж 30 % другого, а 40 % першого на 2 більші від 20 % другого. Знайти ці числа.
9. Сума квадратів двох від'ємних чисел дорівнює 74, а різниця їх квадратів 24. Знайти ці числа.
10. Якщо розсадити дітей по двоє за стіл, то не вистачить три столи. Якщо ж розсадити їх по троє, то один стіл виявиться зайвим. Скільки було дітей і скільки столів?