Коренем n-го степеня (корінь n-го степеня - n-th root) з числа a називається таке число, n-й степінь якого дорівнює a.
Арифметичним коренем (арифметичний корінь - arithmetical root) n-го степеня з числа a називають невід'ємне число, n-й степінь якого дорівнює a.
Арифметичний корінь n-го степеня з числа a позначають
| Наприклад | 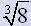 | =2, тому що 23=8 і 2>0. |
При парному n існує два корені n-го степеня з будь-якого додатного числа a; корінь n-го степеня з числа 0 дорівнює 0; коренів парного степеня з від'ємних чисел не існує. При непарному n існує корінь n-го степеня з будь-якого числа a, і притому тільки один.
Для коренів непарного степеня справджується рівність
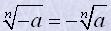
Наприклад
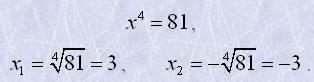
Для будь-якого x
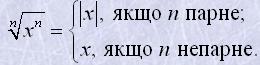
Корінь другого степеня з числа називають квадратним коренем (квадратний корінь - square root), а показник 2 кореня в запису опускають (наприклад, корінь квадратний із 7 позначають просто
).
Корінь третього степеня називають кубічним коренем (кубічний корінь - cube root).
Основні властивості арифметичних коренів -го степеня.
 |  |
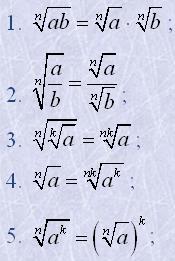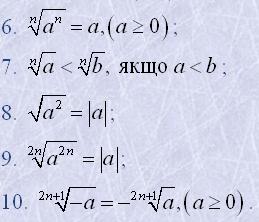Степенем числа a>0 з раціональним показником
, де m - ціле число, а n - натуральне (n>1), називається число 
.
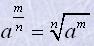
Якщо a<0, раціональний степінь числа a не визначений.
Для будь-яких r, s і додатних a і b справедливі рівності:
| 1. a0=1; |  |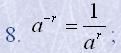
| 2. a1=a; | 9. Якщо 0 |
| 3. ay·a5=ay+5; | ay |
| 4. ay:a5=ay-5; | ay>by, якщо r<0; |
| 5. (ay)5=ay5; | 10. Якщо r>s, то |
| 6. (ab)y=ayby; | ay>a5, якщо a>1, |
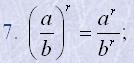 | ay |
Приклад 1
| Спростити вираз |  |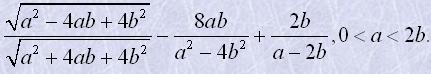
Розв'язання
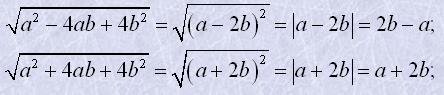
Тоді
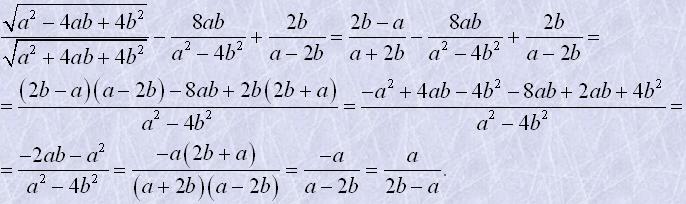
Приклад 2
Перевірити справедливість рівності
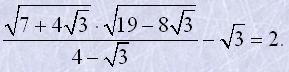
Розв'язання
Розглянемо рівність
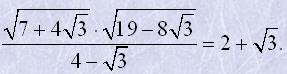
Очевидно, що коли вона виконується, то виконується і задана рівність.
| Нехай |  |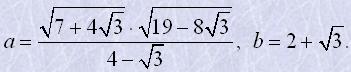
Неважко переконатись, що a>0 і b>0. Якщо при цьому виконується рівність a2=b2, nj a=b.
Знаходимо
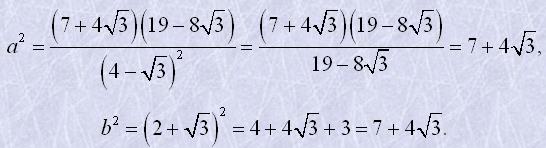
Оскільки a2=b2 то a=b, тобто задана рівність справедлива.
Вправи
1. Добути корінь з одночленів:
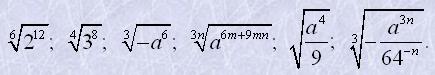
2. Винести множник з-під знака кореня:
 |  |
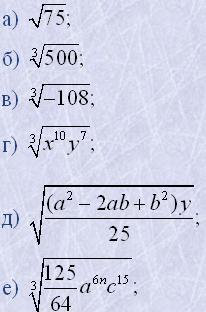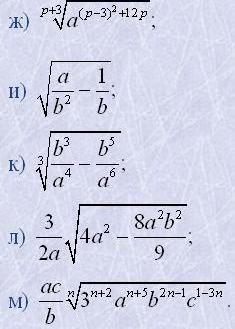3. Внести множник під знак кореня:
 |  |
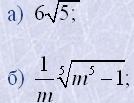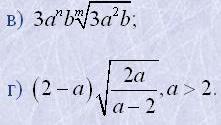4. Скоротити показники коренів та підкореневих виразів:
 |  |
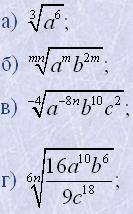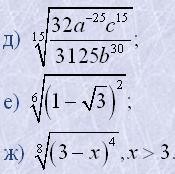5. Привести корені до загального показника:
 |  |
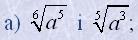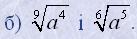6. Звільнити підкореневий вираз від дробу:
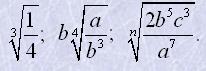
7. Що більше:
8. Виконати дії:
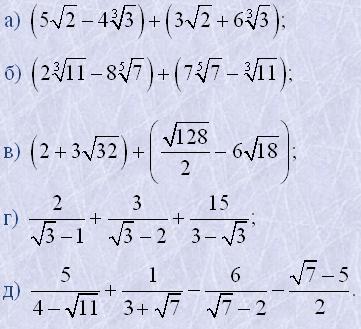
9. Виконати множення:
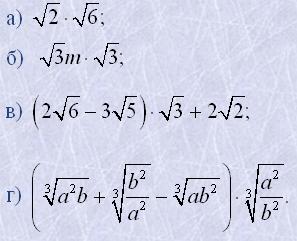
10. Виконати дії:
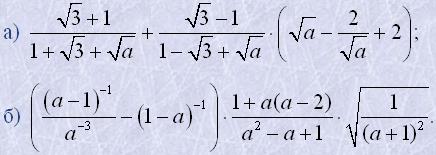
11. Виконати ділення:
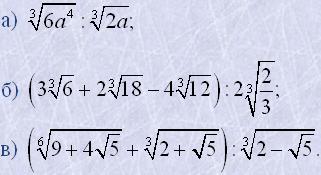
12. Виконати дії:
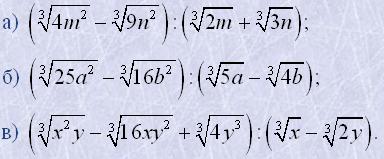
13. Піднести до степеня такі вирази:
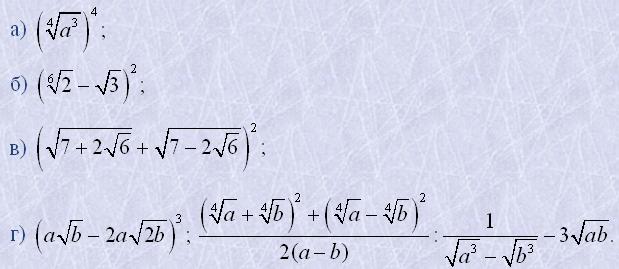
14. Скоротити дроби:
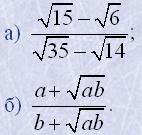
15. Звільнити дроби від коренів у знаменнику:
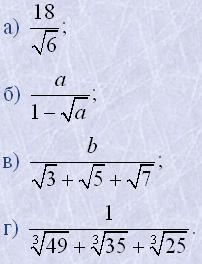
16. Довести тотожності:
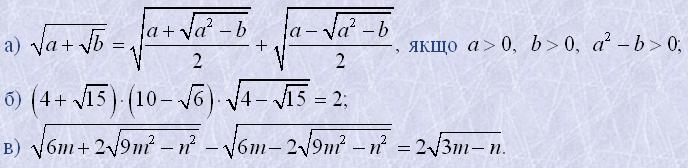
17. Виконати дії:
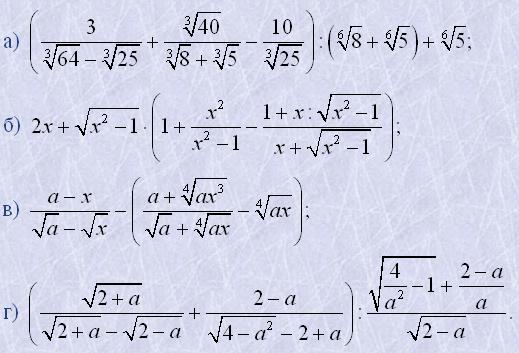
18. Спростити вирази:
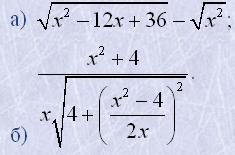
19. Довести тотожності:
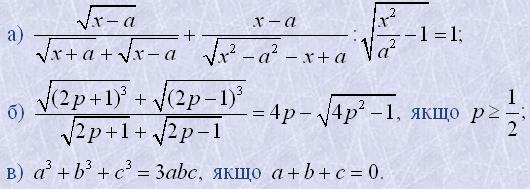
20. Написати без коренів такі вирази:
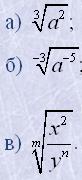
21. Замінити радикалами:
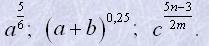
22. Обчислити:
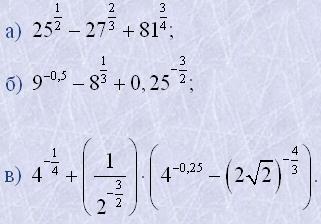
23. Виконати дії:
24. Довести рівності:
|  |
 |
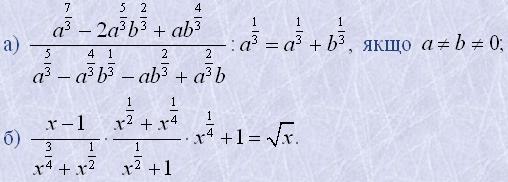